摘要：8．在⊿ABC中.AB⊥AC.AD⊥BC.D是垂足.则.类似有命题:三棱锥A-BCD(图2)中.AD⊥平面ABC.AO⊥平面BCD.O为垂足.且O在⊿BCD内.则.上述命题是 ( ) A. 真命题 B. 假命题 C. 增加AB⊥AC的条件才是真命题 D. 增加三棱锥A-BCD是正三棱锥的 条件才是真命题
网址：http://m.1010jiajiao.com/timu3_id_4463102[举报]
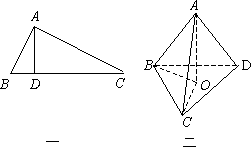
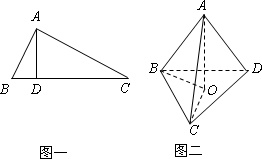
如图一，在△ABC中，AB⊥AC、AD⊥BC，D是垂足，则AB2＝BD·BC(射影定理)．类似有命题：三棱锥A－BCD(图二)中，AD⊥平面ABC，AO⊥平面BCD，O为垂足，且O在△BCD内，则
，
上述命题是
[ ]
A．真命题
B．假命题
C．增加“AB⊥AC”的条件才是真命题
D．增加“三棱锥A－BCD是正三棱锥”的条件才是真命题
如图一，在△ABC中，AB⊥AC、AD⊥BC，D是垂足，则AB2＝BD·BC(射影定理)．类似有命题：三棱锥A－BCD(图二)中，AD⊥平面ABC，AO⊥平面BCD，O为垂足，且O在△BCD内，则S2△ABC＝S2△BCO·S2△BCD．上述命题是
[ ]
A．真命题
B．假命题
C．增加“AB⊥AC”的条件才是真命题
D．增加“三棱锥A－BCD是正三棱锥”的条件才是真命题
如图甲，在△ABC中，AB⊥AC，AD⊥BC，D为．垂足，则AB2=BD•BC，该结论称为射影定理．如图乙，在三棱锥A-BCD中，AD⊥平面ABC，AO⊥平面BCD，O为垂足，且O在△BCD内，类比射影定理，探究S△ABC、S△BCO、S△BCD这三者之间满足的关系是S△ABC2=S△BCO•S△BCD
S△ABC2=S△BCO•S△BCD
．
