摘要: 已知函数f(x)=(a.b.cN).f的图象按向量=平移后得到的图象关于原点对称. (1)求a.b.c的值, (2)设0〈〈1.0〈1.求证, (3)设x是正实数.nN,求证2n-2
网址:http://m.1010jiajiao.com/timu3_id_4462845[举报]
(本小题满分12分)已知函数f(x)=x2-1(x≥1)的图象是C1,函数y=g(x)的图象C2与C1关于直线y=x对称.
(1)求函数y=g(x)的解析式及定义域M;
(2)对于函数y=h(x),如果存在一个正的常数a,使得定义域A内的任意两个不等的值x1,x2都有|h(x1)-h(x2)|≤a|x1-x2|成立,则称函数y=h(x)为A的利普希茨Ⅰ类函数.试证明:y=g(x)是M上的利普希茨Ⅰ类函数;
(3)设A、B是曲线C2上任意不同两点,证明:直线AB与直线y=x必相交.
(1)求函数y=g(x)的解析式及定义域M;
(2)对于函数y=h(x),如果存在一个正的常数a,使得定义域A内的任意两个不等的值x1,x2都有|h(x1)-h(x2)|≤a|x1-x2|成立,则称函数y=h(x)为A的利普希茨Ⅰ类函数.试证明:y=g(x)是M上的利普希茨Ⅰ类函数;
(3)设A、B是曲线C2上任意不同两点,证明:直线AB与直线y=x必相交.
(本小题满分12分)
已知函数f(x)=2sinωx·cos(ωx+)+(ω>0)的最小正周期为4π.
(1)求正实数ω的值;
(2)在△ABC中,内角A、B、C的对边分别为a、b、c,且满足2bcosA=acosC+ccosA,求f(A)的值.
已知函数f(x)=2sinωx·cos(ωx+)+(ω>0)的最小正周期为4π.
(1)求正实数ω的值;
(2)在△ABC中,内角A、B、C的对边分别为a、b、c,且满足2bcosA=acosC+ccosA,求f(A)的值.
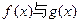 图象交于不同的两点;
图象交于不同的两点;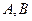 ,求线段AB在x轴上的射影A1B1的长的取值范围。
,求线段AB在x轴上的射影A1B1的长的取值范围。
 ,求△ABC的面积.
,求△ABC的面积.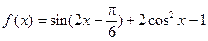
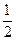 ,求△ABC的面积.
,求△ABC的面积.