摘要：解:(Ⅰ)设P(x0,y0)是y=f(x)图象上点.Q(x,y),则. ∴ ∴-y=loga(x+2a-3a).∴y=loga (x＞a) 5分 (Ⅱ) ∴x＞3a ∵f(x)与g(x)在［a+2,a+3］上有意义. ∴3a＜a+2 ∴0＜a＜1 6分 ∵|f(x)-g(x)|≤1恒成立|loga(x-3a)(x-a)|≤1恒成立. 8分 对x∈［a+2,a+3］上恒成立.令h(x)=(x-2a)2-a2 其对称轴x=2a,2a＜2,2＜a+2 ∴当x∈［a+2,a+3］ hmin(x)=h(a+2).hmax=h(a+3) ∴原问题等价 10分 12分
网址：http://m.1010jiajiao.com/timu3_id_4462806[举报]
设函数y=f(x)=ax+
(a≠0)的图象过点（0，-1）且与直线y=-1有且只有一个公共点；设点P（x0，y0）是函数y=f（x）图象上任意一点，过点P分别作直线y=x和直线x=1的垂线，垂足分别是M，N．
（1）求y=f（x）的解析式；
（2）证明：曲线y=f（x）的图象是一个中心对称图形，并求其对称中心Q；
（3）证明：线段PM，PN长度的乘积PM•PN为定值；并用点P横坐标x0表示四边形QMPN的面积．． 查看习题详情和答案>>
| 1 | x+b |
（1）求y=f（x）的解析式；
（2）证明：曲线y=f（x）的图象是一个中心对称图形，并求其对称中心Q；
（3）证明：线段PM，PN长度的乘积PM•PN为定值；并用点P横坐标x0表示四边形QMPN的面积．． 查看习题详情和答案>>
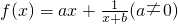的图象过点（0，-1）且与直线y=-1有且只有一个公共点；设点P（x0，y0）是函数y=f（x）图象上任意一点，过点P分别作直线y=x和直线x=1的垂线，垂足分别是M，N．