摘要:设函数,给出以下四个论断: (Ⅰ)它的图象关于直线对称, (Ⅱ)它的图象关于点(.0)对称, (Ⅲ)它的周期为π, (Ⅳ)它在区间[-.0]上是增函数. 以其中的两个论断为条件.余下的论断为结论.写出你认为正确的两个命题.并对其中一个命题加以证明. 数列{an}的前n项和为Sn.又数列{bn}满足bn=(r为确定的值).求r的值.并证明{an}是等差数列. 如图. 边长为a的菱形ABCD中.A=60°.又PA⊥面ABCD.PA=a,E为CP中点. (Ⅰ)求证:面BDE⊥面ABCD, (Ⅱ)求PB与面BDE所成的角大小, (Ⅲ)求二面角B-DE-C的大小. 现有流量均为300m3/s的两条河流A.B.汇合于某处后.不断混合.它们的含沙量分别为2kg/m3和0.2kg/m3.假若从汇合处开始.沿岸设有若干个观测点.两股水流在汇经相邻两个观测点的过程中.其混合效果相当于两股水流在1秒钟内交流100m3的水量.即从A股流入B股100m3水.经混合后.又从B股流入A股100m3水并混合. (Ⅰ)问从第几个观测点开始.两股河水的含沙量之差小于0.01?kg/m3., (Ⅱ)随着两股水流的不断混合.它们的含沙量趋向于一个常数.试求出这个常数. 已知A.B是椭圆上的两个点.O为坐标原点. (Ⅰ)若OA⊥OB.|AB|=.求直线OA.OB的方程, 若OA⊥OB.求△AOB面积的最小值. 设f(x)=ax2+bx+c(a,b,c∈R)在区间[0.1]上恒有|f(x)|≤1. (Ⅰ)对所有这样的f(x).求|a|+|b|+|c|最大值, (Ⅱ)试给出一个这样的f(x).使|a|+|b|+|c|确定达到上述最大值. 已知一次函数y=kx+c(c>0).二次函数y=x2的图象交于A.B两点. (Ⅰ)若k.c为已知常数.求线段AB长度|AB|, (Ⅱ)若k.c为变动的实数时(c>0).求证: 仅当0<c<1时.有两个k值使|AB|=2.
网址:http://m.1010jiajiao.com/timu3_id_4462370[举报]
设函数 ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线x= 对称;
对称;
②它的图象关于点 对称;
对称;
③它的周期是π;
④在区间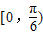 上是增函数.
上是增函数.
以其中两个论断作为条件,余下的一个论断作为结论,写出你认为正确的命题:
条件 结论 ;(用序号表示) 查看习题详情和答案>>
 ,给出以下四个论断:
,给出以下四个论断:①它的图象关于直线x=
 对称;
对称; ②它的图象关于点
 对称;
对称;③它的周期是π;
④在区间
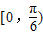 上是增函数.
上是增函数.以其中两个论断作为条件,余下的一个论断作为结论,写出你认为正确的命题:
条件 结论 ;(用序号表示) 查看习题详情和答案>>
设函数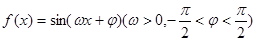 ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线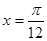 对称; ③它的最小正周期是
对称; ③它的最小正周期是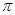 ;
;
②它的图象关于点( ,0)对称;④在区间[
,0)对称;④在区间[ ]上是增函数.
]上是增函数.
以其中两个论断作为条件,余下论断作为结论,写出一个正确的命题:
条件_ ▲ _ ,结论_▲ (填序号)
查看习题详情和答案>>
设函数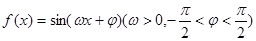 ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线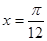 对称; ③它的最小正周期是
对称; ③它的最小正周期是 ;
;
②它的图象关于点(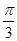 ,0)对称;
④在区间[
,0)对称;
④在区间[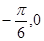 ]上是增函数.
]上是增函数.
以其中两个论断作为条件,余下论断作为结论,写出一个正确的命题:
条件_ ▲ _ ,结论_ ▲ (填序号).
查看习题详情和答案>>
 ,给出以下四个论断:
,给出以下四个论断: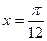 对称; ③它的最小正周期是
对称; ③它的最小正周期是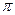 ;
;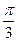 ,0)对称;④在区间[
,0)对称;④在区间[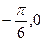 ]上是增函数.
]上是增函数.