题目内容
设函数 ,给出以下四个论断:
,给出以下四个论断:①它的图象关于直线x=
 对称;
对称; ②它的图象关于点
 对称;
对称;③它的周期是π;
④在区间
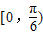 上是增函数.
上是增函数.以其中两个论断作为条件,余下的一个论断作为结论,写出你认为正确的命题:
条件 结论 ;(用序号表示)
【答案】分析:先由③知ω=2,再由对称轴,可得函数解析式,然后判断对称性和单调性是否成立即可.
解答:解:若③函数的周期是π,则可得ω=2,
所以f(x)=sin(2x+φ),
若①图象关于直线x= 对称,则
对称,则 ,解得
,解得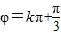 ,
,
因为 ,所以
,所以 .
.
所以 ,
,
由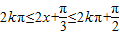 ,得
,得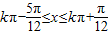 ,
,
即函数单调区间[kπ-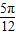 ,kπ+
,kπ+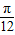 ](k∈z),
](k∈z),
因为当k=0时,单调区间为[ ].
].
所以在区间 上函数不是增函数,所以④不正确.
上函数不是增函数,所以④不正确.
当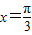 时,
时, ,所以它的图象关于点
,所以它的图象关于点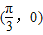 对称,所以②正确.
对称,所以②正确.
所以①③⇒②.
故答案为:条件①③,结论②.
点评:本题主要考查三角函数的性质,考查学生分析问题的能力,综合性较强.
解答:解:若③函数的周期是π,则可得ω=2,
所以f(x)=sin(2x+φ),
若①图象关于直线x=
 对称,则
对称,则 ,解得
,解得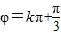 ,
,因为
 ,所以
,所以 .
.所以
 ,
,由
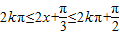 ,得
,得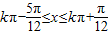 ,
,即函数单调区间[kπ-
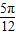 ,kπ+
,kπ+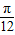 ](k∈z),
](k∈z),因为当k=0时,单调区间为[
 ].
].所以在区间
 上函数不是增函数,所以④不正确.
上函数不是增函数,所以④不正确.当
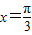 时,
时, ,所以它的图象关于点
,所以它的图象关于点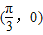 对称,所以②正确.
对称,所以②正确.所以①③⇒②.
故答案为:条件①③,结论②.
点评:本题主要考查三角函数的性质,考查学生分析问题的能力,综合性较强.

练习册系列答案
相关题目
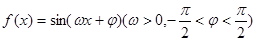 ,给出以下四个论断:
,给出以下四个论断: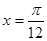 对称; ③它的最小正周期是
对称; ③它的最小正周期是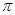 ;
; ,0)对称;④在区间[
,0)对称;④在区间[ ]上是增函数.
]上是增函数.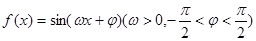 ,给出以下四个论断:
,给出以下四个论断: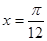 对称; ③它的最小正周期是
对称; ③它的最小正周期是 ;
;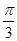 ,0)对称;
④在区间[
,0)对称;
④在区间[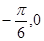 ]上是增函数.
]上是增函数.