摘要:已知=.求的值. 已知等比数列的公比为.前n项的和为.且..成等差数列. (Ⅰ)求的值, (Ⅱ)求证成等差数列. 一个口袋中装有大小相同的2个白球和3个黑球. (Ⅰ)从中摸出两个球.求两球恰好颜色不同的概率, (Ⅱ)从中摸出一个球.放回后再摸出一个球.求两球恰好颜色不同的概率. 注意:考生在两题中选一题作答.如果两题都答.只以计分. (甲)如图.正三棱柱的底面边长为.点在边上.是以点M为直角顶点的等腰直角三角形. (Ⅰ) 求证点为边的中点, (Ⅱ) 求点到平面的距离, (Ⅲ) 求二面角的大小. (乙) 如图.直三棱柱ABC-A1B1C1中.底面是以∠ABC为直角的等腰直角三角形.AC=.BB1=.D为A1C1的中点.E为B1C的中点. (Ⅰ)求直线BE与A1C所成的角, (Ⅱ)在线段AA1上是否存在点F.使CF⊥平面B1DF.若存在.求出,若不存在.说明理由. 已知双曲线:.是右顶点,是右焦点, 点在轴正半轴上.且满足成等比数列,过作双曲线在第一.三象限的渐近线的垂线.垂足为. (Ⅰ)求证:, (Ⅱ)若与双曲线的左.右两支分别相交于点..求双曲线的离心率的取值范围. 设函数..且方程+1=0有实根. (Ⅰ)证明:, (Ⅱ)证明:, (Ⅲ)若是方程+1=0的一个实根.判断的正负并加以证明. 高考数学模拟试卷2参考解答及评分标准 说明:
网址:http://m.1010jiajiao.com/timu3_id_4461099[举报]
 ,
, .
.  ,且
,且 ,求
,求 的值;
的值; 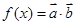 ,求
,求 的周期及单调减区间.
的周期及单调减区间.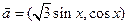 ,
,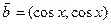 .
.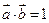 ,且
,且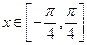 ,求
,求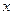 的值;
的值; 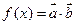 ,求
,求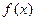 的周期及单调减区间.
的周期及单调减区间. (本小题满分12分)已知
(本小题满分12分)已知