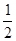摘要：20． 已知f(x)是定义在上的奇函数.当x＜0时.f(x)=x2-x-2.解不等式f(x)＞0． 解: 设x＞0.则 -x＜0． ∴ f (-x)=(-x)2-(-x)-2=x2+x-2． 而f (x) 是奇函数. ∴ f (-x)=-f (x). 于是 f (x)=-x2-x+2.x＞0． ∴ (1) 由 得 ． (2) 由 得 ． 综上所述.不等式f (x)＞0的解集为{x∣x＜-1或0＜x＜1．
网址：http://m.1010jiajiao.com/timu3_id_4461094[举报]
(本小题满分12分)
已知函数f(x)＝lg(ax－bx)(a>1>b>0)．
(1)求y＝f(x)的定义域；
(2)在函数y＝f(x)的图象上是否存在不同的两点，使得过这两点的直线平行于x轴；
(3)当a，b满足什么条件时，f(x)在(1，＋∞)上恒取正值．
查看习题详情和答案>>
(本小题满分12分)已知函数f(x)=x2－1(x≥1)的图象是C1，函数y=g(x)的图象C2与C1关于直线y=x对称.
(1)求函数y=g(x)的解析式及定义域M；
(2)对于函数y=h(x)，如果存在一个正的常数a，使得定义域A内的任意两个不等的值x1，x2都有|h(x1)－h(x2)|≤a|x1－x2|成立，则称函数y=h(x)为A的利普希茨Ⅰ类函数.试证明：y=g(x)是M上的利普希茨Ⅰ类函数；
(3)设A、B是曲线C2上任意不同两点，证明：直线AB与直线y=x必相交.
(1)求函数y=g(x)的解析式及定义域M；
(2)对于函数y=h(x)，如果存在一个正的常数a，使得定义域A内的任意两个不等的值x1，x2都有|h(x1)－h(x2)|≤a|x1－x2|成立，则称函数y=h(x)为A的利普希茨Ⅰ类函数.试证明：y=g(x)是M上的利普希茨Ⅰ类函数；
(3)设A、B是曲线C2上任意不同两点，证明：直线AB与直线y=x必相交.
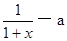，(f／(x))是f(x)的导数）