摘要：如图.在三棱锥P-ABC中.PA⊥底面ABC.△ABC为正三角形.D.E分别是BC.CA的中点. (1)证明:平面PBE⊥平面PAC, (2)如何在BC上找一点F.使AD//平面PEF?并说明理由, 中的点F.求三棱锥B-PEF的体积.
网址：http://m.1010jiajiao.com/timu3_id_4461018[举报]
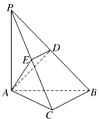如图，在三棱锥P-ABC中，PA⊥底面ABC，PA=AB，∠ABC=60°，∠BCA=90°，点D、E分别在棱PB、PC上，且DE∥BC．（1）求证：BC⊥平面PAC；
（2）当D为PB的中点时，求AD与平面PAC所成的角的正弦值；
（3）是否存在点E使得二面角A-DE-P为直二面角？并说明理由． 查看习题详情和答案>>
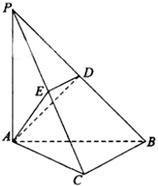如图，在三棱锥P-ABC中，PA⊥底面ABC，PA=AB，∠ABC=60°，∠BCA=90°，点D，E分别在棱PB，PC上，且DE∥BC，（Ⅰ）求证：BC⊥平面PAC；
（Ⅱ）当D为PB的中点时，求AD与平面PAC所成的角的余弦值． 查看习题详情和答案>>
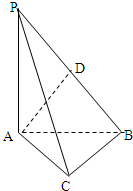如图，在三棱锥P-ABC中，PA⊥底面ABC，PA=AB，∠ABC=60°，∠BCA=90°，点D在棱PB上．（1）求证：BC⊥平面PAC；
（2）当D为PB中点时，求AD与平面PAC所成的角的大小． 查看习题详情和答案>>
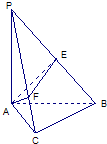如图，在三棱锥P-ABC中，PA⊥底面ABC，∠ACB=90°，AE⊥PB于E，AF⊥PC于F，若PA=PB=2，∠BPC=θ，则当△AEF的面积为
如图，在三棱锥P-ABC中，PA⊥底面ABC，∠ACB=90°，AE⊥PB于E，AF⊥PC于F，若PA=AB=2，∠BPC=θ，则当△AEF的面积最大时，tanθ的值为（ ）