摘要:17.证明:不等式成立.(n∈N)
网址:http://m.1010jiajiao.com/timu3_id_4460737[举报]
考察等式:
 (*)
(*)
其中n,m,r∈N*,r≤m<n且r≤n-m,
某同学用概率论方法证明等式(*)如下:设一批产品共有n件,其中m件是次品,其余为正品,现从中随机取出r件产品,记事件Ak={取到的r件产品中恰有k件次品},则 ,k=0,1,…,r。显然A0,A1,…,Ar为互斥事件,且
,k=0,1,…,r。显然A0,A1,…,Ar为互斥事件,且 (必然事件),因此
(必然事件),因此
 ,
,
所以, ,即等式(*)成立。
,即等式(*)成立。
对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.
现有以下四个判断:①等式(*)成立;②等式(*)不成立;③证明正确;④证明不正确,试写出所有正确判断的序号( )。
查看习题详情和答案>>
 (*)
(*)其中n,m,r∈N*,r≤m<n且r≤n-m,
某同学用概率论方法证明等式(*)如下:设一批产品共有n件,其中m件是次品,其余为正品,现从中随机取出r件产品,记事件Ak={取到的r件产品中恰有k件次品},则
 ,k=0,1,…,r。显然A0,A1,…,Ar为互斥事件,且
,k=0,1,…,r。显然A0,A1,…,Ar为互斥事件,且 (必然事件),因此
(必然事件),因此
 ,
,所以,
 ,即等式(*)成立。
,即等式(*)成立。对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.
现有以下四个判断:①等式(*)成立;②等式(*)不成立;③证明正确;④证明不正确,试写出所有正确判断的序号( )。
已知命题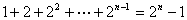 及其证明:
及其证明:
(1)当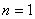 时,左边=1,右边=
时,左边=1,右边=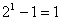 所以等式成立;
所以等式成立;
(2)假设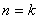 时等式成立,即
时等式成立,即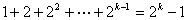 成立,
成立,
则当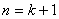 时,
时,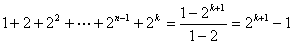 ,所以
,所以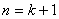 时等式也成立。
时等式也成立。
由(1)(2)知,对任意的正整数n等式都成立。
经判断以上评述
A.命题、推理都正确 B命题不正确、推理正确
C.命题正确、推理不正确 D命题、推理都不正确
查看习题详情和答案>>
 }的前n项和为
}的前n项和为 , 已知对任意的
, 已知对任意的 ,点
,点 均在函数
均在函数 (
( 且
且 ,b,r均为常数)的图像上。
,b,r均为常数)的图像上。 ,证明:对任意的
,证明:对任意的 ,不等式
,不等式 成立。
成立。 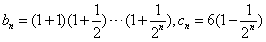 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,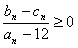 。
。 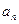 }的前n项和为
}的前n项和为 ,已知对任意的
,已知对任意的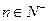 ,点
,点 ,均在函数
,均在函数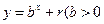 且
且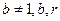 均为常数)的图像上。
均为常数)的图像上。 ,证明:对任意的
,证明:对任意的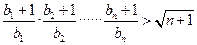 成立。
成立。