摘要:11.如图.∠ABC=∠ACB,CD⊥AC于C,BE⊥AB 于B.AE交BC于F.且BE=CD.下列结论不一定正确的是 A.AB=AC B. ∠BAE=∠CAD C.AE=AD D.BF=EF
网址:http://m.1010jiajiao.com/timu3_id_446067[举报]
Rt△ABC中,∠ACB=90°,CD为高线,点E在边BC上,且BE=2EC,连接AE,EF⊥AE,与边AB相交于点F.
(1)如图1,当tan∠BAC=1时,求证:EF=2EG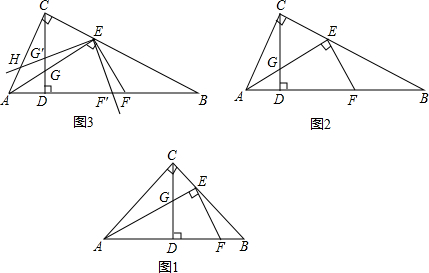
(2)如图2,当tan∠BAC=2时,则线段EF、EG的数量关系为______;
(3)如图3,在(2)的条件下,将∠FEG绕点E顺时针旋转α,旋转后EF边所在的直线与边AB相交于点F′,EG边所在的直线与边AC相交于点H,与高线CD相交于点G′,若AH=3 ,且
,且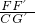 =
= ,求线段G′H的长.
,求线段G′H的长.
查看习题详情和答案>>
Rt△ABC中,∠ACB=90°,CD为高线,点E在边BC上,且BE=2EC,连接AE,EF⊥AE,与边AB相交于点F.
(1)如图1,当tan∠BAC=1时,求证:EF=2EG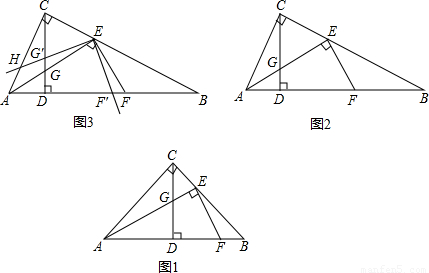
(2)如图2,当tan∠BAC=2时,则线段EF、EG的数量关系为______;
(3)如图3,在(2)的条件下,将∠FEG绕点E顺时针旋转α,旋转后EF边所在的直线与边AB相交于点F′,EG边所在的直线与边AC相交于点H,与高线CD相交于点G′,若AH=3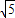 ,且
,且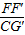 =
= ,求线段G′H的长.
,求线段G′H的长.
查看习题详情和答案>>
(1)如图1,当tan∠BAC=1时,求证:EF=2EG

(2)如图2,当tan∠BAC=2时,则线段EF、EG的数量关系为______;
(3)如图3,在(2)的条件下,将∠FEG绕点E顺时针旋转α,旋转后EF边所在的直线与边AB相交于点F′,EG边所在的直线与边AC相交于点H,与高线CD相交于点G′,若AH=3
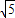 ,且
,且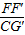 =
= ,求线段G′H的长.
,求线段G′H的长.查看习题详情和答案>>
(2011•南岗区一模)Rt△ABC中,∠ACB=90°,CD为高线,点E在边BC上,且BE=2EC,连接AE,EF⊥AE,与边AB相交于点F.
(1)如图1,当tan∠BAC=1时,求证:EF=2EG
(2)如图2,当tan∠BAC=2时,则线段EF、EG的数量关系为
(3)如图3,在(2)的条件下,将∠FEG绕点E顺时针旋转α,旋转后EF边所在的直线与边AB相交于点F′,EG边所在的直线与边AC相交于点H,与高线CD相交于点G′,若AH=3
,且
=
,求线段G′H的长.
查看习题详情和答案>>
(1)如图1,当tan∠BAC=1时,求证:EF=2EG

(2)如图2,当tan∠BAC=2时,则线段EF、EG的数量关系为
EF=EG
EF=EG
;(3)如图3,在(2)的条件下,将∠FEG绕点E顺时针旋转α,旋转后EF边所在的直线与边AB相交于点F′,EG边所在的直线与边AC相交于点H,与高线CD相交于点G′,若AH=3
| 5 |
| FF′ |
| CG′ |
| 2 |
| 7 |
 ,求∠ACQ的正切值.
,求∠ACQ的正切值.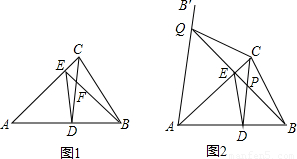
 ,连接DE.
,连接DE.