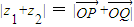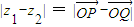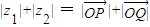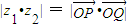摘要： 设A.B.C分别是复数,,对应的不共线三点. 证:曲线与中平行于AC的中位线只有一个公共点.并求出此点.
网址：http://m.1010jiajiao.com/timu3_id_4460330[举报]
设A、B、C分别是复数Z0=ai，Z1=
+bi，Z2=1+ci（其中a，b，c都是实数）对应的不共线的三点．
证明：曲线：Z=Z0cos4t+2Z1cos2tsin2t+Z2sin4t （t∈R）与△ABC中平行于AC的中位线只有一个公共点，并求出此点．
查看习题详情和答案>>
| 1 | 2 |
证明：曲线：Z=Z0cos4t+2Z1cos2tsin2t+Z2sin4t （t∈R）与△ABC中平行于AC的中位线只有一个公共点，并求出此点．
设A、B、C分别是复数Z0=ai，Z1=
+bi，Z2=1+ci（其中a，b，c都是实数）对应的不共线的三点．
证明：曲线：Z=Z0cos4t+2Z1cos2tsin2t+Z2sin4t （t∈R）与△ABC中平行于AC的中位线只有一个公共点，并求出此点．
查看习题详情和答案>>
| 1 |
| 2 |
证明：曲线：Z=Z0cos4t+2Z1cos2tsin2t+Z2sin4t （t∈R）与△ABC中平行于AC的中位线只有一个公共点，并求出此点．
设A、B、C分别是复数Z=ai，Z1=
+bi，Z2=1+ci（其中a，b，c都是实数）对应的不共线的三点．
证明：曲线：Z=Zcos4t+2Z1cos2tsin2t+Z2sin4t （t∈R）与△ABC中平行于AC的中位线只有一个公共点，并求出此点．
查看习题详情和答案>>
+bi，Z2=1+ci（其中a，b，c都是实数）对应的不共线的三点．证明：曲线：Z=Zcos4t+2Z1cos2tsin2t+Z2sin4t （t∈R）与△ABC中平行于AC的中位线只有一个公共点，并求出此点．
查看习题详情和答案>>
设O为坐标原点，复数z1、z2在复平面内对应的点分别为P、Q，则下列结论中不一定正确的是（ ）
A、|z1+z2| = |
| ||||
B、|z1-z2| = |
| ||||
C、|z1|+|z2| = |
| ||||
D、|z1•z2| = |
|
