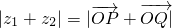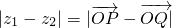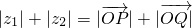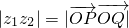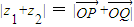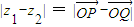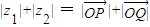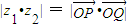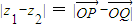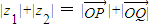题目内容
设O为坐标原点，复数z1、z2在复平面内对应的点分别为P、Q，则下列结论中不一定正确的是（ ）
A、|z1+z2| = |
| ||||
B、|z1-z2| = |
| ||||
C、|z1|+|z2| = |
| ||||
D、|z1•z2| = |
|
分析：用复数的几何意义：复数与复平面内以原点为起点的向量一一对应．
解答：解：∵复数z1、z2在复平面内对应的点分别为P、Q
又∵O为坐标原点
∴复数z1、z2在复平面内对应的向量为
，
∴选项A，B，C都对
由排除法知选项D不一定正确，例如z1=1，z2=i，|z1•z2| = 1， |
•
=0，
故选D．
又∵O为坐标原点
∴复数z1、z2在复平面内对应的向量为
| OP |
| OQ |
∴选项A，B，C都对
由排除法知选项D不一定正确，例如z1=1，z2=i，|z1•z2| = 1， |
| OP |
| OQ| |
故选D．
点评：本题考查复数的几何意义．
练习册系列答案
阅读快车系列答案
相关题目
