摘要：(I)当时.上的点P(与上的点Q( 关于对称.则 此时代入 得)上是偶函数 当时. ------------5分 (II)命题条件等价于因为为偶函数.所以只需考虑的情况. 求导 由(舍)----------8分 ①当0<<1.即时 0 (0.) (.1) 1 + - 0 -4+2 ②当.即时.上单调递增 综上.存在使得的图象的最高点在直线上.-----14分
网址：http://m.1010jiajiao.com/timu3_id_4459378[举报]
记平面内与两定点A1（-2，0），A2（2，0）连线的斜率之积等于常数m（其中m＜0）的动点B的轨迹，加上A1，A2两点所构成的曲线为C
（I）求曲线C的方程，并讨论C的形状与m的值的关系；
（Ⅱ）当m=-
时，过点F（1，0）且斜率为k（k#0）的直线l1交曲线C于M．N两点，若弦MN的中点为P，过点P作直线l2交x轴于点Q，且满足
•
=0．试求
的取值范围．
查看习题详情和答案>>
（I）求曲线C的方程，并讨论C的形状与m的值的关系；
（Ⅱ）当m=-
| 3 |
| 4 |
| MN |
| PQ |
|
| ||
|
|
记平面内与两定点A1（-2，0），A2（2，0）连线的斜率之积等于常数m（其中m＜0）的动点B的轨迹，加上A1，A2两点所构成的曲线为C
（I）求曲线C的方程，并讨论C的形状与m的值的关系；
（Ⅱ）当m=-
时，过点F（1，0）且斜率为k（k#0）的直线l1交曲线C于M．N两点，若弦MN的中点为P，过点P作直线l2交x轴于点Q，且满足
•
=0．试求
的取值范围．
查看习题详情和答案>>
（I）求曲线C的方程，并讨论C的形状与m的值的关系；
（Ⅱ）当m=-
| 3 |
| 4 |
| MN |
| PQ |
|
| ||
|
|
记平面内与两定点A1（-2，0），A2（2，0）连线的斜率之积等于常数m（其中m＜0）的动点B的轨迹，加上A1，A2两点所构成的曲线为C
（I）求曲线C的方程，并讨论C的形状与m的值的关系；
（Ⅱ）当m=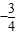
时，过点F（1，0）且斜率为k（k#0）的直线l1交曲线C于M．N两点，若弦MN的中点为P，过点P作直线l2交x轴于点Q，且满足
•
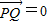．试求
的取值范围．
查看习题详情和答案>>
（I）求曲线C的方程，并讨论C的形状与m的值的关系；
（Ⅱ）当m=
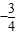时，过点F（1，0）且斜率为k（k#0）的直线l1交曲线C于M．N两点，若弦MN的中点为P，过点P作直线l2交x轴于点Q，且满足•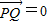．试求的取值范围．查看习题详情和答案>>
的两个焦点分别为
,
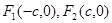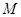是椭圆上一点，且满足
。 
。
的直线l与椭圆C相交于不同的两点A、B，Q为AB的中点，问A、B两点能否关于过点P（0，
）、Q的直线对称？若能，求出
的取值范围；若不能，请说明理由。
的两个焦点分别为
,
是椭圆上一点，且满足
。 
。
的直线l与椭圆C相交于不同的两点A、B，Q为AB的中点，问A、B两点能否关于过点P（0，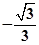
）、Q的直线对称？若能，求出
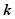的取值范围；若不能，请说明理由。