题目内容
记平面内与两定点A1(-2,0),A2(2,0)连线的斜率之积等于常数m(其中m<0)的动点B的轨迹,加上A1,A2两点所构成的曲线为C(I)求曲线C的方程,并讨论C的形状与m的值的关系;
(Ⅱ)当m=
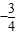 时,过点F(1,0)且斜率为k(k#0)的直线l1交曲线C于M.N两点,若弦MN的中点为P,过点P作直线l2交x轴于点Q,且满足
时,过点F(1,0)且斜率为k(k#0)的直线l1交曲线C于M.N两点,若弦MN的中点为P,过点P作直线l2交x轴于点Q,且满足 •
•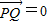 .试求
.试求 的取值范围.
的取值范围.
【答案】分析:(Ⅰ)设动点M(x,y),由条件可得mx2-y2=4m(x≠±2),对m分m<-1,m=-1,-1<m<0三种情况讨论即可;
(Ⅱ)设出直线l1的方程为y=k(x-1),代入椭圆方程,利用韦达定理,确定|MN|、|PQ|,即可求得结论.
解答:解:(I)设动点B(x,y).
当x≠±2时,由条件可得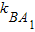 •
•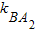 =
=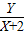 •
•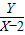 =
=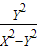 =m
=m
即mx2-y2=4m(x≠±2).
又A1(-2,0)、A2(2,0)的坐标满足mx2-y2=4m.
当m<-1时,曲线C的方程为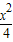 +
+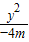 =1,曲线C是焦点在y轴上的椭圆;
=1,曲线C是焦点在y轴上的椭圆;
当m=-1时,曲线C的方程为x2+y2=4,曲线C是圆心在原点上的圆;
当-1<m<0时,曲线C的方程为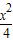 +
+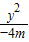 =1,曲线C是焦点在x轴上的椭圆;
=1,曲线C是焦点在x轴上的椭圆;
(Ⅱ)由(I)知,曲线C的方程为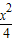 +
+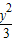 =1.
=1.
依题意,直线l1的方程为y=k(x-1).
代入椭圆方程可得:(3+4k2)x2-8k2x+4k2-12=0
设M(x1,y1),N(x2,y2),则
由韦达定理得:x1+x2=-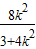 ,x1x2=
,x1x2=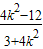
∴弦MN的中点为P(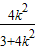 ,
,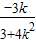 )
)
∴|MN|=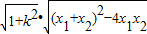 =
=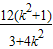
直线l2的方程为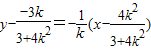
由y=0,可得x=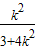 ,则Q(
,则Q(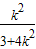 ,0),
,0),
∴|PQ|=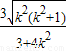
∴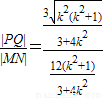 =
=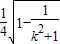
∵k2+1>1,∴0<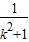 <1
<1
∴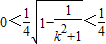
∴ 的取值范围为(0,
的取值范围为(0, ).
).
点评:本题考查直线与圆锥曲线的综合问题,着重考查圆锥曲线的轨迹问题,突出化归思想、分类讨论思想、方程思想的考查,综合性强.
(Ⅱ)设出直线l1的方程为y=k(x-1),代入椭圆方程,利用韦达定理,确定|MN|、|PQ|,即可求得结论.
解答:解:(I)设动点B(x,y).
当x≠±2时,由条件可得
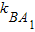 •
•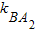 =
=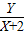 •
•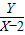 =
=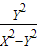 =m
=m即mx2-y2=4m(x≠±2).
又A1(-2,0)、A2(2,0)的坐标满足mx2-y2=4m.
当m<-1时,曲线C的方程为
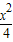 +
+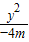 =1,曲线C是焦点在y轴上的椭圆;
=1,曲线C是焦点在y轴上的椭圆;当m=-1时,曲线C的方程为x2+y2=4,曲线C是圆心在原点上的圆;
当-1<m<0时,曲线C的方程为
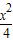 +
+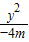 =1,曲线C是焦点在x轴上的椭圆;
=1,曲线C是焦点在x轴上的椭圆;(Ⅱ)由(I)知,曲线C的方程为
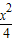 +
+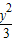 =1.
=1.依题意,直线l1的方程为y=k(x-1).
代入椭圆方程可得:(3+4k2)x2-8k2x+4k2-12=0
设M(x1,y1),N(x2,y2),则
由韦达定理得:x1+x2=-
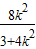 ,x1x2=
,x1x2=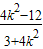
∴弦MN的中点为P(
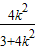 ,
,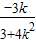 )
)∴|MN|=
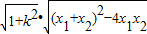 =
=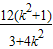
直线l2的方程为
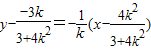
由y=0,可得x=
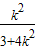 ,则Q(
,则Q(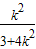 ,0),
,0),∴|PQ|=
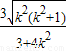
∴
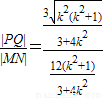 =
=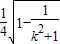
∵k2+1>1,∴0<
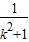 <1
<1∴
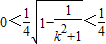
∴
 的取值范围为(0,
的取值范围为(0, ).
).点评:本题考查直线与圆锥曲线的综合问题,着重考查圆锥曲线的轨迹问题,突出化归思想、分类讨论思想、方程思想的考查,综合性强.

练习册系列答案
相关题目