摘要：9．分析:本题属信息迁移题,考查学生灵活应用知识的能力. 解:设靠近A的长轴端点为M.另一长轴的端点为N.若小球沿AM方向运动,则路程应为2(a-c),若小球沿ANM方向运动,则路程为2(a+c),若小球不沿AM与AN方向运动,则路程应为4a. 答案:D
网址：http://m.1010jiajiao.com/timu3_id_4459097[举报]
（2010•桂林二模）（注意：在试题卷上作答无效）桂林某学校从参加高三年级第二次模拟考试的学生中随机抽出100名学生，将其数学成绩（均为整数）分成五段[50，70），[70，90），[90，110），[110，130），[130，150]后得到如右部分频率分布直方图，分析图形的信息，回答下列问题：
（Ⅰ）求分数在[90，110）内的频率和学生数，并补全这个频率分布直方图；
（Ⅱ）现从分数段[90，150]的学生中随机抽取2人给予助学金奖励，抽到的学生成绩在[90，110）内每人奖励100元，在[100，130）内每人奖励200元，在[130，150）内每人奖励300元，用ξ表示抽取结束后总的奖励金额，求ξ的分布列和数学期望．
（注意：在试题卷上作答无效）
桂林某学校从参加高三年级第二次模拟考试的学生中随机抽出100名学生，将其数学成绩（均为整数）分成五段[50，70），[70，90），[90，110），[110，130），[130，150]后得到如右部分频率分布直方图，分析图形的信息，回答下列问题：
（Ⅰ）求分数在[90，110）内的频率和学生数，并补全这个频率分布直方图；
（Ⅱ）现从分数段[90，150]的学生中随机抽取2人给予助学金奖励，抽到的学生成绩在[90，110）内每人奖励100元，在[100，130）内每人奖励200元，在[130，150）内每人奖励300元，用ξ表示抽取结束后总的奖励金额，求ξ的分布列和数学期望．
查看习题详情和答案>>
桂林某学校从参加高三年级第二次模拟考试的学生中随机抽出100名学生，将其数学成绩（均为整数）分成五段[50，70），[70，90），[90，110），[110，130），[130，150]后得到如右部分频率分布直方图，分析图形的信息，回答下列问题：
（Ⅰ）求分数在[90，110）内的频率和学生数，并补全这个频率分布直方图；
（Ⅱ）现从分数段[90，150]的学生中随机抽取2人给予助学金奖励，抽到的学生成绩在[90，110）内每人奖励100元，在[100，130）内每人奖励200元，在[130，150）内每人奖励300元，用ξ表示抽取结束后总的奖励金额，求ξ的分布列和数学期望．
查看习题详情和答案>>
A，x＋1桂林某学校从参加高三年级第二次模拟考试的学生中随机抽出100名学生，将其数学成绩(均为整数)分成五段[50，70)，[70，90)，[90，110)，[110，130)，[130，150]后得到如下部分频率分布直方图，分析图形的信息，回答下列问题：
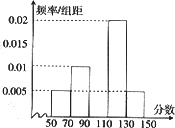
(Ⅰ)求分数在[90，110)内的频率和学生数，并补全这个频率分布直方图；
(Ⅱ)现从分数段[90，150]的学生中随机抽取2人给予助学金奖励，抽到的学生成绩在[90，110)内每人奖励100元，在[100，130)内每人奖励200元，在[130，150)内每人奖励300元，用ξ表示抽取结束后总的奖励金额，求ξ的分布列和数学期望
表示运算符号)：当m、n都是正偶数或都是正奇数时，m
n＝m＋n，如4
6＝4＋6＝10，3