摘要:22. 已知关于的方程的两个根为.设函数. ① 判断在上的单调性, ② 若.证明.
网址:http://m.1010jiajiao.com/timu3_id_4459065[举报]
(本题满分14分
已知椭圆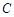 :
: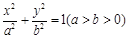 的离心率为
的离心率为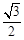 ,以原点为圆心,
,以原点为圆心,
椭圆的短半轴长为半径的圆与直线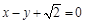 相切.
相切.
⑴求椭圆C的方程;
⑵设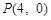 ,
,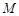 、
、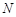 是椭圆
是椭圆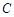 上关于
上关于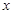 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结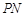 交椭圆
交椭圆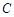
于另一点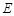 ,求直线
,求直线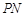 的斜率的取值范围;
的斜率的取值范围;
⑶在⑵的条件下,证明直线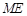 与
与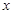 轴相交于定点.
轴相交于定点.
查看习题详情和答案>>
(本题满分14分
已知椭圆 :
: 的离心率为
的离心率为 ,以原点为圆心,
,以原点为圆心,
椭圆的短半轴长为半径的圆与直线 相切.
相切.
⑴求椭圆C的方程;
⑵设 ,
, 、
、 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆
于另一点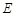 ,求直线
,求直线 的斜率的取值范围;
的斜率的取值范围;
⑶在⑵的条件下,证明直线 与
与 轴相交于定点.
轴相交于定点.
已知椭圆
 :
: 的离心率为
的离心率为 ,以原点为圆心,
,以原点为圆心,椭圆的短半轴长为半径的圆与直线
 相切.
相切.⑴求椭圆C的方程;
⑵设
 ,
, 、
、 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆
于另一点
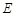 ,求直线
,求直线 的斜率的取值范围;
的斜率的取值范围;⑶在⑵的条件下,证明直线
 与
与 轴相交于定点.
轴相交于定点.(本题满分14分)已知函数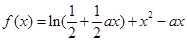 (
(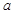 为常数,
为常数,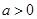 ).
).
(Ⅰ)当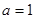 时,求函数
时,求函数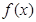 在
在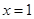 处的切线方程;
处的切线方程;
(Ⅱ)当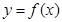 在
在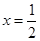 处取得极值时,若关于
处取得极值时,若关于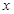 的方程
的方程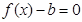 在[0,2]上恰有两个不相等的实数根,求实数
在[0,2]上恰有两个不相等的实数根,求实数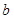 的取值范围;
的取值范围;
(Ⅲ)若对任意的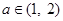 ,总存在
,总存在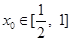 ,使不等式
,使不等式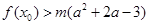 成立,求实数
成立,求实数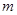 的取值范围.
的取值范围.
查看习题详情和答案>>
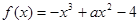
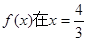 处取得极值,求实数a的值;
处取得极值,求实数a的值;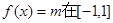 上恰有两个不同的实数根,求实数m的取值范围;
上恰有两个不同的实数根,求实数m的取值范围;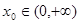 ,使得不等式
,使得不等式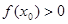 成立,求实数a的取值范围。
成立,求实数a的取值范围。 (
(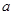 是常数)
是常数)  的单调区间;
的单调区间; 在
在 处取得极值时,若关于x的方程
处取得极值时,若关于x的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数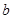 的取值范围;
的取值范围;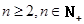 时
时 .
.