摘要:若(2x+)4=a0+a1x+a2x2+a3x3+a4 x4.则(a0+a2+a4)2-(a1+a3)2的值为( ) A.1 B.-1 C.0 D.2
网址:http://m.1010jiajiao.com/timu3_id_4458946[举报]
(文科做)已知直线l1:mx+ny+4=0,l2:(m-1)x+y+n=0,l1经过(-1,-1),问l1∥l2是否成立?若成立,求出m,n的值,若不成立,说明理由.
(理科做)△ABC的顶点B(3,4),AB边上的高CE所在直线方程为2x+3y-16=0,BC边上的中线AD所在直线方程为2x-3y+1=0,求AC的长.
查看习题详情和答案>>
(理科做)△ABC的顶点B(3,4),AB边上的高CE所在直线方程为2x+3y-16=0,BC边上的中线AD所在直线方程为2x-3y+1=0,求AC的长.
已知平面内两定点F1(0,-
)、F2(0,
),动点P满足条件:|
|-|
|=4,设点P的轨迹是曲线E,O为坐标原点.
(I)求曲线E的方程;
(II)若直线y=k(x+1)与曲线E相交于两不同点Q、R,求
•
的取值范围;
(III)(文科做)设A、B两点分别在直线y=±2x上,若
=λ
(λ∈[
,3]),记xA、xB分别为A、B两点的横坐标,求|xA•xB|的最小值.
(理科做)设A、B两点分别在直线y=±2x上,若
=λ
(λ∈[
,3]),求△AOB面积的最大值.
查看习题详情和答案>>
| 5 |
| 5 |
| PF1 |
| PF2 |
(I)求曲线E的方程;
(II)若直线y=k(x+1)与曲线E相交于两不同点Q、R,求
| OQ |
| OR |
(III)(文科做)设A、B两点分别在直线y=±2x上,若
| AP |
| PB |
| 1 |
| 2 |
(理科做)设A、B两点分别在直线y=±2x上,若
| AP |
| PB |
| 1 |
| 2 |
(13分,理科做)已知函数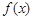 的定义域为
的定义域为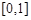 ,且同时满足:①
,且同时满足:①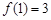 ;②
;②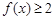 恒成立;③若
恒成立;③若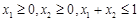 ,则有
,则有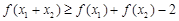 .
.
(1)试求函数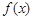 的最大值和最小值;
的最大值和最小值;
(2)试比较 与
与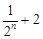 的大小
的大小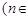 N);
N);
(3)某人发现:当x= (nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1
(nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1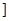 ,都有
,都有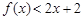 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
查看习题详情和答案>>