摘要:19.(1)设.由.得 . .3分 于是...成等差数列等价于 6分 所以点的轨迹是以原点为圆心.为半径的圆, 7分 (2)设直线的方程为... 直线与曲线相切..即①. 9分 由.同理. 的中点. 10分 是以为底边的等腰三角形. .即②. 12分 由①②解得. 14分
网址:http://m.1010jiajiao.com/timu3_id_4458555[举报]
对于函数![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 的生成函数.
的生成函数.
(1)下面给出两组函数,![]() 是否分别为
是否分别为![]() 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组:![]() ;
;
第二组:![]() ;
;
(2)设![]() ,生成函数
,生成函数![]() .若不等式
.若不等式
![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,取
,取![]() ,生成函数
,生成函数![]() 使
使![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(12分) 设函数 (
(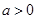 ),
), .
.
(1) 将函数 图象向右平移一个单位即可得到函数
图象向右平移一个单位即可得到函数 的图象,试写出
的图象,试写出 的解析式及值域;
的解析式及值域;
(2) 关于 的不等式
的不等式 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数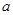 的取值范围;
的取值范围;
(3) 对于函数 与
与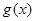 定义域上的任意实数
定义域上的任意实数 ,若存在常数
,若存在常数 ,使得
,使得 和
和 都成立,则称直线
都成立,则称直线 为函数
为函数 与
与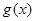 的“分界线”.设
的“分界线”.设 ,
, ,试探究
,试探究 与
与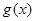 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
查看习题详情和答案>>
设函数![]() (
(![]() ),
),![]() .
.
(1) 将函数![]() 图象向右平移一个单位即可得到函数
图象向右平移一个单位即可得到函数![]() 的图象,试写出
的图象,试写出![]() 的解析式及值域;
的解析式及值域;
(2) 关于![]() 的不等式
的不等式![]() 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数![]() 的取值范围;
的取值范围;
(3) 对于函数![]() 与
与![]() 定义域上的任意实数
定义域上的任意实数![]() ,若存在常数
,若存在常数![]() ,使得
,使得![]() 和
和![]() 都成立,则称直线
都成立,则称直线![]() 为函数
为函数![]() 与
与![]() 的“分界线”.设
的“分界线”.设![]() ,
,![]() ,试探究
,试探究![]() 与
与![]() 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
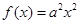 (
(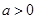 ),
),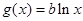 .
.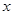 的不等式
的不等式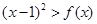 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数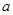 的取值范围;
的取值范围;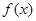 与
与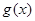 定义域上的任意实数
定义域上的任意实数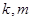 ,使得
,使得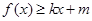 和
和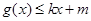 都成立,则称直线
都成立,则称直线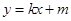 为函数
为函数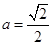 ,
,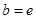 ,试探究
,试探究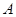 和获得等级不是
和获得等级不是 、
、 、
、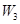 ,物理、化学、生物获得等级不是
,物理、化学、生物获得等级不是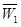 、
、 、
、 .
.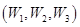 );
); ,并说明理由.
,并说明理由.