摘要：17．解:(1)由1的解集有且只有一个元素知 或 --------------- 当时.函数在上递增.此时不满足条件2 综上可知 ---------------- -------------- (2)由条件可知-------------- 当时.令或 所以或----------------------- 又时.也有----------- 综上可得数列的变号数为3-----------------
网址：http://m.1010jiajiao.com/timu3_id_4455965[举报]
已知二次函数
同时满足：①不等式
≤0的解集有且只有一个元素；②在定义域内存在
，使得不等式
成立，设数列｛
｝的前
项和
．
（1）求函数的表达式；
(2) 设各项均不为0的数列｛
｝中，所有满足
的整数
的个数称为这个数列｛｝的变号数，令
（
）,求数列｛｝的变号数；
（3）设数列｛
｝满足：
，试探究数列｛｝是否存在最小项？若存在，求出该项，若不存在，说明理由．
已知二次函数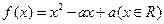
同时满足：①不等式
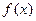≤0的解集有且只有一个元素；②在定义域内存在
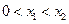，使得不等式
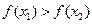成立，设数列｛
｝的前
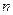项和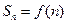
．
（1）求函数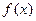的表达式；
(2) 设各项均不为0的数列｛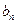
｝中，所有满足
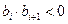的整数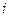
的个数称为这个数列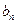｛｝的变号数，令
（
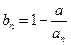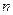
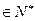）,求数列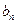｛｝的变号数；
（3）设数列｛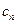
｝满足：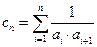
，试探究数列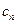｛｝是否存在最小项？若存在，求出该项，若不存在，说明理由．
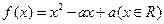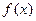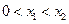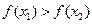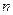同时满足：①不等式≤0的解集有且只有一个元素；②在定义域内存在，使得不等式成立，设数列｛｝的前项和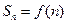．（1）求函数
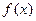的表达式；(2) 设各项均不为0的数列｛
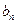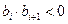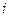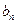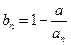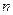
｝中，所有满足的整数的个数称为这个数列｛｝的变号数，令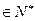（）,求数列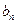｛｝的变号数； （3）设数列｛
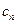｝满足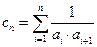：，试探究数列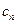｛｝是否存在最小项？若存在，求出该项，若不存在，说明理由．
已知二次函数f（x）=x2-ax+a（x∈R）同时满足：①不等式f（x）≤0的解集有且只有一个元素；②在定义域内存在0＜x1＜x2，使得不等式f（x1）＞f（x2）成立．设数列{an}的前n项和Sn=f（n），
（1）求数列{an}的通项公式；
（2）试构造一个数列{bn}，（写出{bn}的一个通项公式）满足：对任意的正整数n都有bn＜an，且
=2，并说明理由；
（3）设各项均不为零的数列{cn}中，所有满足ci-ci+1＜0的正整数i的个数称为这个数列{cn}的变号数．令cn=1-
（n为正整数），求数列{cn}的变号数．
查看习题详情和答案>>
（1）求数列{an}的通项公式；
（2）试构造一个数列{bn}，（写出{bn}的一个通项公式）满足：对任意的正整数n都有bn＜an，且
| lim |
| n→∞ |
| an |
| bn |
（3）设各项均不为零的数列{cn}中，所有满足ci-ci+1＜0的正整数i的个数称为这个数列{cn}的变号数．令cn=1-
| a |
| an |
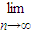
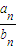=2，并说明理由；
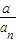（n为正整数），求数列{cn}的变号数．
=2，并说明理由；
（n为正整数），求数列{cn}的变号数．