摘要:16.对于在区间[a.b]上有意义的两个函数与.如果对于任意.均有|.则称与在[a.b]上是接近的. 若函数与函数在区间[a.b]上非常接近.则该区间可以是 .(写出一个符合条件的区间即可)
网址:http://m.1010jiajiao.com/timu3_id_4455741[举报]
对于在区间[a,b]上有意义的两个函数m(x)与n(x),如果对于区间[a,b]中的任意x均有|m(x)-n(x)|≤1,则称m(x)与n(x)在[a,b]上是“密切函数”,[a,b]称为“密切区间”,若函数m(x)=x2-3x+4与n(x)=2x-3在区间[a,b]上是“密切函数”,则b-a的最大值为 .
查看习题详情和答案>>
对于在区间[a,b]上有意义的两个函数f(x)和g(x),如果对任意x∈[a,b],均有|f(x)-g(x)|≤1,那么我们称f(x)和g(x)在[a,b]上是接近的.若f(x)=log2(ax+1)与g(x)=log2x在闭区间[1,2]上是接近的,则a的取值范围是
查看习题详情和答案>>
[0,1]
[0,1]
.对于在区间[a,b]上有意义的两个函数f(x)和g(x),如果对任意x∈[a,b],均有|f(x)-g(x)|≤1,那么我们称f(x)和g(x)在[a,b]上是接近的.若f(x)=log2(cx+1)与g(x)=log2x在闭区间[1,2]上是接近的,则c的取值范围是( )
查看习题详情和答案>>
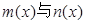 ,如果对于区间[a,b]中的任意x均有
,如果对于区间[a,b]中的任意x均有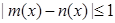 ,则称
,则称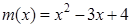 与
与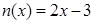 在区间[a,b]上是“密切函数”,则
在区间[a,b]上是“密切函数”,则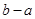 的最大值为 .
的最大值为 .