摘要: 时.∴---理1分.文2分 时. ∴---理3分.文5分 ∴通项公式---理5分.文7分 (2)当时. ∴---理6分.文9分 时. ∴---理7分.文11分 ∴ ---理9分.文14分 (3)∵,---理10分 两边同时乘以2n,得即∴数列{+4}是以6为首项.4为公比的等比数列.+4 = 6×4n-1.∴ ---理13分 又C1=1, 满足上式 ∴通项公式---理14分 法二: = = -- = = 又C1=1, 满足上式 ∴通项公式
网址:http://m.1010jiajiao.com/timu3_id_4455481[举报]
(本小题满分14分)
已知定义域为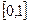 的函数
的函数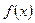 同时满足以下三个条件:
同时满足以下三个条件:
① 对任意的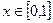 ,总有
,总有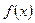 ≥0; ②
≥0; ②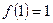 ;
;
③若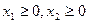 且
且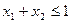 ,则有
,则有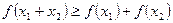 成立,并且称
成立,并且称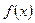 为“友谊函数”,
为“友谊函数”,
请解答下列各题:
(1)若已知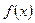 为“友谊函数”,求
为“友谊函数”,求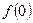 的值;
的值;
(2)函数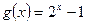 在区间
在区间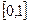 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知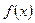 为“友谊函数”,且
为“友谊函数”,且 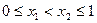 ,求证:
,求证: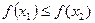
(本小题满分14分)
已知:函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, 为实数).
为实数).
(1)当 时,求
时,求 的解析式;
的解析式;
(2)若 ,试判断
,试判断 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)是否存在 ,使得当
,使得当 有最大值1?若存在,求出
有最大值1?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看习题详情和答案>>
(本小题满分14分)已知 (
( ,
, 为此函数的定义域)同时满足下列两个条件:①函数
为此函数的定义域)同时满足下列两个条件:①函数 在
在 内单调递增或单调递减;②如果存在区间
内单调递增或单调递减;②如果存在区间 ,使函数
,使函数 在区间
在区间 上的值域为
上的值域为 ,那么称
,那么称 ,
, 为闭函数;
为闭函数;
请解答以下问题:
(1) 求闭函数 符合条件②的区间
符合条件②的区间 ;
;
(2) 判断函数 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若 是闭函数,求实数
是闭函数,求实数 的取值范围;
的取值范围;
查看习题详情和答案>>
 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, 为实数).
为实数). 时,求
时,求 ,试判断
,试判断 上的单调性,并证明你的结论;
上的单调性,并证明你的结论; ,使得当
,使得当 有最大值1?若存在,求出
有最大值1?若存在,求出 (
( ,
, 为此函数的定义域)同时满足下列两个条件:①函数
为此函数的定义域)同时满足下列两个条件:①函数 在
在 ,使函数
,使函数 上的值域为
上的值域为 符合条件②的区间
符合条件②的区间 是否为闭函数?并说明理由;
是否为闭函数?并说明理由; 是闭函数,求实数
是闭函数,求实数 的取值范围;
的取值范围;