（2006•崇文区一模）已知数列{a_n}满足

an

an-1

=

n+1

n-1

(n∈N*，n＞1)，a₁=2
（I）求证：数列{a_n}的通项公式为a_n=n（n+1）
（II）求数列{

1

an

}的前n项和T_n；
（III）是否存在无限集合M，使得当n∈M时，总有|Tn-1|＜

1

10

成立．若存在，请找出一个这样的集合；若不存在，请说明理由．

（2006•崇文区一模）已知数列{a_n}满足3S_n=（n+2）a_n（n∈N^*），其中S_n为其前n项的和，a₁=2
（I）证明：数列{a_n}的通项公式为a_n=n（n+1）；
（II）求数列{

1

an

}的前n项和T_n；
（III）是否存在无限集合M，使得当n∈M时，总有|Tn-1|＜

1

10

成立，若存在，请找出一个这样的集合；若不存在，请说明理由．

（2011•朝阳区二模）对于整数a，b，存在唯一一对整数q和r，使得a=bq+r，0≤r＜|b|．特别地，当r=0时，称b能整除a，记作b|a，已知A={1，2，3，…，23}．
（Ⅰ）存在q∈A，使得2011=91q+r（0≤r＜91），试求q，r的值；
（Ⅱ）若B⊆A，card（B）=12（card（B）指集合B 中的元素的个数），且存在a，b∈B，b＜a，b|a，则称B为“谐和集”．请写出一个含有元素7的“谐和集”B₀和一个含有元素8的非“谐和集”C，并求最大的m∈A，使含m的集合A有12个元素的任意子集为“谐和集”，并说明理由．

已知：函数f（x）=a•lnx+bx²+x在点（f，f（1））处的切线方程为x-y-1=0．
（1）求f（x）的表达式；
（2）设函数y=

1

2

f(x)+

x(x-1)

2

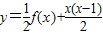的反函数为p（x），t（x）=p（x）（1-x），求函数t（x）的最大值；
（3）在（2）中，问是否存在正整数N，使得当n∈N₊且n＞N时，不等式p(-1)+p(-

1

2

)+p(-

1

3

) +p(-

1

n

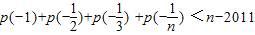) ＜n-2011恒成立？若存在，请找出一个满足条件的N的值，并给以说明；若不存在，请说明理由．