摘要：16．已知:如下图.梯形ABCD中.AD∥BC.AB=CD.对角线AC与BD相交于点O.则图中全等三角形共有 对．
网址：http://m.1010jiajiao.com/timu3_id_445385[举报]
已知：如图，在梯形ABCD中，AD∥BC，∠DCB=90°，E是AD的中点，点P是BC边上的动点（不与点B重合），EP与BD相交于点O．
（1）当P点在BC边上运动时，求证：△BOP∽△DOE；
（2）设（1）中的相似比为k，若AD：BC=2：3．请探究：当k为下列三种情况时，四边形ABPE是什么四边形？①当k=1时，是 ；②当k=2时，是 ；③当k=3时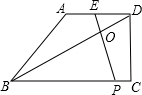
，是 ．并证明k=2时的结论．
查看习题详情和答案>>
（1）当P点在BC边上运动时，求证：△BOP∽△DOE；
（2）设（1）中的相似比为k，若AD：BC=2：3．请探究：当k为下列三种情况时，四边形ABPE是什么四边形？①当k=1时，是
，是
已知：如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，过O点作EF∥A
D分别交AB，CD于点E，F．
（1）下面是小明对“△AOB与△DOC是否相似”的解答：
解：△AOB∽△DOC理由如下：
∵AD∥BC（ ）
∴△AOD∽△COB
∴
=
（ ）
又∵∠AOB=∠DOC（ ）
∴△AOB∽△DOC（ ）
你认为小明的每一步解答过程是否正确？若正确，请在括号内填上理由；若不正确，请在该步骤后面的括号内打“×”．
（2）OE与OF有何关系？为什么？
（3）试求出
+
的值．
查看习题详情和答案>>
D分别交AB，CD于点E，F．（1）下面是小明对“△AOB与△DOC是否相似”的解答：
解：△AOB∽△DOC理由如下：
∵AD∥BC（ ）
∴△AOD∽△COB
∴
| OA |
| OC |
| OD |
| OB |
又∵∠AOB=∠DOC（ ）
∴△AOB∽△DOC（ ）
你认为小明的每一步解答过程是否正确？若正确，请在括号内填上理由；若不正确，请在该步骤后面的括号内打“×”．
（2）OE与OF有何关系？为什么？
（3）试求出
| OE |
| AD |
| OF |
| BC |
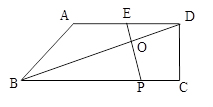
（10分）已知：如图，在梯形ABCD中，AD∥BC，∠DCB = 90°，E是AD的中点，点P是BC边上的动点（不与点B重合），EP与BD相交于点O.
（1）当P点在BC边上运动时，求证：△BOP∽△DOE；
（2）设（1）中的相似比为
，若AD︰BC = 2︰3. 请探究：当k为下列三种情况时，四边形ABPE是什么四边形？
①当= 1时，是 ；
②当= 2时，是 ；
③当= 3时，是 .
请证明= 2时的结论.
查看习题详情和答案>>
，若AD︰BC = 2︰3. 请探究：当k为下列三种情况时，四边形ABPE是什么四边形？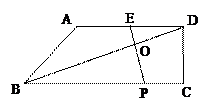
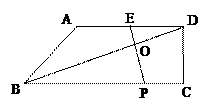
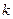，若AD︰BC = 2︰3. 请探究：当k为下列三种情况时，四边形ABPE是什么四边形？①当