摘要：如图.在棱长为1的正方体中.E.F分别是棱 的中点 (1)求点E到面对角线BD的距离 (2)求证:四边形是菱形 21如图.已知点P是边长为1的正方体ABCD所在平面外一点.且PA⊥面ABCD.点E为PD中点 (1)求证:PB∥面EAC, (2)求异面直线PB与AC所成角的取值范围
网址：http://m.1010jiajiao.com/timu3_id_4453044[举报]
（辽宁卷理19）如图，在棱长为1的正方体
中，AP=BQ=b（0<b<1），截面PQEF∥
，截面PQGH∥
．
（Ⅰ）证明：平面PQEF和平面PQGH互相垂直；
（Ⅱ）证明：截面PQEF和截面PQGH面积之和是定值，
并求出这个值；
（Ⅲ）若
与平面PQEF所成的角为
，求与平面PQGH所成角的正弦值．
说明：本小题主要考查空间中的线面关系，面面关系，解三角形等基础知识，考查空间想象能力与逻辑思维能力。满分12分．
查看习题详情和答案>>（辽宁卷理19）如图，在棱长为1的正方体
中，AP=BQ=b（0<b<1），截面PQEF∥
，截面PQGH∥
．
（Ⅰ）证明：平面PQEF和平面PQGH互相垂直；
（Ⅱ）证明：截面PQEF和截面PQGH面积之和是定值，
并求出这个值；
（Ⅲ）若
与平面PQEF所成的角为
，求与平面PQGH所成角的正弦值．
说明：本小题主要考查空间中的线面关系，面面关系，解三角形等基础知识，考查空间想象能力与逻辑思维能力。满分12分．
查看习题详情和答案>>（本小题满分12分）
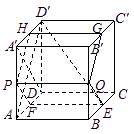如图，在棱长为1的正方体
中，AP=BQ=b（0<b<1），截面PQEF∥
，截面PQGH∥
．
（Ⅰ）证明：平面PQEF和平面PQGH互相垂直；
（Ⅱ）证明：截面PQEF和截面PQGH面积之和是定值，
并求出这个值；
（Ⅲ）若
与平面PQEF所成的角为
，求与平
面PQGH所成角的正弦值．
查看习题详情和答案>>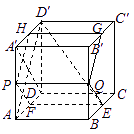
中，AP=BQ=b（0<b<1），截面PQEF∥
，截面PQGH∥
．
，求
与平面PQEF所成角的正弦值．
中，
是侧棱
上的一点，
．
，使直线
与平面
；
上是否存在一个定点
，
在平面
上