摘要：离心率.焦点为F1(1.2).F2(5.2)的椭圆方程是
网址：http://m.1010jiajiao.com/timu3_id_4452452[举报]
F1、F2为椭圆的焦点，P为椭圆上一点，∠F1PF2 = 90°，且| PF2 | < | PF1 |，已知椭圆的离心率为
，则∠PF1F2∶∠PF2F1 =（ ）
设F1、F2是双曲线
-
=1（a＞0，b＞0）的左、右两个焦点，若双曲线右支上存在一点P，使(
+
)•
=0（O为坐标原点），且tan∠PF2F1=2，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| OP |
| OF2 |
| F2P |
已知F1、F2分别是双曲线
－
＝1(a＞0，b＞0)的左、右焦点，P为双曲线上的一点，若∠F1PF2＝90°，且△F1PF2的则三边长成等差数列，则双曲线的离心率是
[ ]
A．
2
B．
3
C．
4
D．
5
－
＝1(a＞0，b＞0)的左、右焦点，P为双曲线上的一点，若∠F1PF2＝90°，且△F1PF2的则三边长成等差数列，则双曲线的离心率是
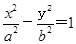的两焦点为F1、F2，点P在双曲线上，∠F1PF2的平分线分线段F1F2的比为5 ：1，则双曲线离心率的取值范围是
]
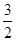B．（1，
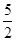] D．（