摘要: 已知P(m.a)是抛物线y=ax2上的点.且点P在第一象限. (1)求m的值 (2)直线y=kx+b过点P.交x轴的正半轴于点A.交抛物线于另一点M. ①当b=2a时.∠OPA=90°是否成立?如果成立.请证明,如果不成立.举出一个反例说明, ②当b=4时.记△MOA的面积为S.求的最大值.
网址:http://m.1010jiajiao.com/timu3_id_445097[举报]
(10分)
如图,在平面直角坐标系中,顶点为(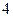 ,
, )的抛物线交
)的抛物线交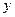 轴于
轴于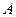 点,交
点,交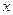 轴于
轴于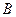 ,
,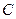 两点(点
两点(点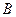 在点
在点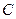 的左侧). 已知
的左侧). 已知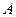 点坐标为(
点坐标为(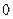 ,
,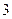 ).
).

(1)求此抛物线的解析式;
(2)过点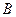 作线段
作线段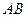 的垂线交抛物线于点
的垂线交抛物线于点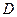 , 如果以点
, 如果以点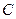 为圆心的圆与直线
为圆心的圆与直线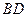 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴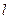 与⊙
与⊙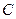 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点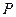 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于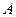 ,
,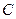 两点之间,问:当点
两点之间,问:当点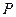 查看习题详情和答案>>
查看习题详情和答案>>
如图,在平面直角坐标系中,顶点为(
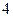 ,
, )的抛物线交
)的抛物线交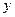 轴于
轴于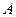 点,交
点,交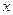 轴于
轴于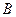 ,
,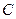 两点(点
两点(点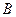 在点
在点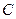 的左侧). 已知
的左侧). 已知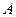 点坐标为(
点坐标为(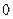 ,
,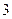 ).
).
(1)求此抛物线的解析式;
(2)过点
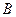 作线段
作线段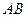 的垂线交抛物线于点
的垂线交抛物线于点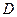 , 如果以点
, 如果以点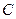 为圆心的圆与直线
为圆心的圆与直线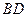 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴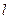 与⊙
与⊙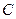 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;(3)已知点
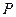 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于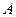 ,
,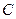 两点之间,问:当点
两点之间,问:当点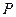 查看习题详情和答案>>
查看习题详情和答案>>
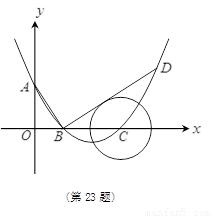
如图,在平面直角坐标系中,顶点为(![]() ,
,![]() )的抛物线交
)的抛物线交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧), 已知
的左侧), 已知![]() 点坐标为(
点坐标为(![]() ,
,![]() )。
)。
(1)求此抛物线的解析式;
(2)过点![]() 作线段
作线段![]() 的垂线交抛物线于点
的垂线交抛物线于点![]() , 如果以点
, 如果以点![]() 为圆心的圆与直线
为圆心的圆与直线![]() 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴![]() 与⊙
与⊙![]() 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点![]() 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于![]() ,
,![]() 两点之间,问:当点
两点之间,问:当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积最大?并求出此时
的面积最大?并求出此时![]() 点的坐标和
点的坐标和![]() 的最大面积.
的最大面积.
 |
查看习题详情和答案>>
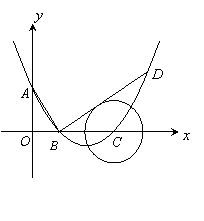
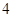 ,
,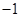 )的抛物线交
)的抛物线交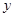 轴于
轴于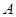 点,交
点,交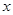 轴于
轴于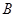 ,
,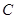 两点(点
两点(点 ,
, ).
).
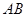 的垂线交抛物线于点
的垂线交抛物线于点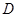 ,
如果以点
,
如果以点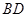 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴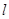 与⊙
与⊙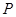 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于