摘要:例1如图1.矩形ABCD.AD=a.AB=b.要使BC边上至少存在一点P.使△ABP.△APD.△CDP两两相似.则a,b间的关系一定满足 图1 A. a≥b, B.a≥b, C. a≥b, D.a≥2b. 分析:由于矩形是轴对称图形.根据其对称性可知.通常情况下点P的位置有两个.它们关于BC的垂直平分线对称,如果存在一点P.则该点必为BC的中点.此时△ABP≌△DCP.则AP=DP.△APD为等腰直角三角形.要使△ABP.△APD.△CDP两两相似.则它们都是等腰直角三角形. 此时..即a=2b. 当点P的位置有两个时.a>2b. 总之.a≥2b.故选D. 例2如图2.已知点是边长为4的正方形内一点.且..垂足是.请在射线上找一点.使以点..为顶点的三角形与相似(请注意:全等图形是相似图形的特例) . 图2 分析:由于对应点没有确定.所以需分类讨论. (1)若△MBC∽.则需在射线上截取线段.连结. . . ∴-. (2)若△CBM∽.则需在射线上截取线段.连结. . ∴在射线上取或时..都为符合条件的.
网址:http://m.1010jiajiao.com/timu3_id_444692[举报]
(2004 陕西)如图所示,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系一定满足
[ ]
|
A. |
B. |
C. |
D. |
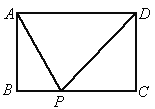
(2004•陕西)如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )

A.a≥ b
b
B.a≥b
C.a≥ b
b
D.a≥2b
查看习题详情和答案>>

A.a≥
 b
bB.a≥b
C.a≥
 b
bD.a≥2b
查看习题详情和答案>>
(2004•陕西)如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
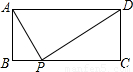
A.a≥ b
b
B.a≥b
C.a≥ b
b
D.a≥2b
查看习题详情和答案>>

A.a≥
 b
bB.a≥b
C.a≥
 b
bD.a≥2b
查看习题详情和答案>>
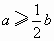
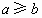
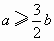
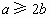
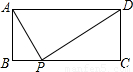
 b
b b
b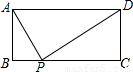
 b
b b
b