摘要：2．难点:能应用上述概念.定理解决有关问题.培养学生的综合解题能力. 教法.学法.和教具
网址：http://m.1010jiajiao.com/timu3_id_444125[举报]
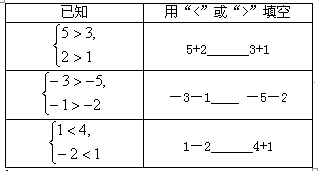
我们知道不等式的两边加（或减）同一个数（或式子）不等号的方向不变、不等式组是否也具有类似的性质？完成下列填空：
一般地，如果
．那么a+c b+d．（用“＞”或“＜”填空）你能应用不等式的性质证明上述关系式吗？
查看习题详情和答案>>
一般地，如果
|
| 已知 | 用“＜”或“＞”填空 | |||||
|
5+2 | |||||
|
-3-1 | |||||
|
1-2 |
我们知道三角形的一条中线能将这个三角形分成面积相等的两个三角形，反之，若经过三角形的一个顶点引一条直线将这个三角形分成面积相等两个三角形，那么这条直线平分三角形的这个顶点的对边．如图1，若S△ABD=S△ADC，则BD=CD成立．
请你直接应用上述结论解决以下问题：
（1）已知：如图2，AD是△ABC的中线，沿AD翻折△ADC，使点C落在点E，DE交AB于F，若△ADE与△ADB重叠部分面积等于△ABC面积的
，问线段AE与线段BD有什么关系？在图中按要求画出图形，并说明理由．
（2）已知：如图3，在△ABC中，∠ACB=90°，AC=2，AB=4，点D是AB边的中点，点P是BC边上的任意一点，连接PD，沿PD翻折△ADP，使点A落在E，若△PDE与△PDB重叠部分的面积等于△ABP面积的
，直接写出BP2的值．
查看习题详情和答案>>
请你直接应用上述结论解决以下问题：
（1）已知：如图2，AD是△ABC的中线，沿AD翻折△ADC，使点C落在点E，DE交AB于F，若△ADE与△ADB重叠部分面积等于△ABC面积的
| 1 |
| 4 |
（2）已知：如图3，在△ABC中，∠ACB=90°，AC=2，AB=4，点D是AB边的中点，点P是BC边上的任意一点，连接PD，沿PD翻折△ADP，使点A落在E，若△PDE与△PDB重叠部分的面积等于△ABP面积的
| 1 |
| 4 |
回答下列问题：
（1）如图所示的甲、乙两个平面图形能折什么几何体？
（2）由多个平面围成的几何体叫做多面体．若一个多面体的面数为f，顶点个数为v，棱数为e，分别计算第（1）题中两个多面体的f+v-e的值？你发现什么规律？
（3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数．
查看习题详情和答案>>
（1）如图所示的甲、乙两个平面图形能折什么几何体？
（2）由多个平面围成的几何体叫做多面体．若一个多面体的面数为f，顶点个数为v，棱数为e，分别计算第（1）题中两个多面体的f+v-e的值？你发现什么规律？
（3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数．
那么a+c b+d．（用“>”或“<”填空）你能应用不等式的性质证明上述关系式吗？
那么a+c b+d．（用“>”或“<”填空）你能应用不等式的性质证明上述关系式吗？