题目内容
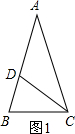
我们知道三角形的一条中线能将这个三角形分成面积相等的两个三角形,反之,若经过三角形的一个顶点引一条直线将这个三角形分成面积相等两个三角形,那么这条直线平分三角形的这个顶点的对边.如图1,若S△ABD=S△ADC,则BD=CD成立.
请你直接应用上述结论解决以下问题:

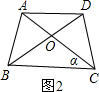
(1)已知:如图2,AD是△ABC的中线,沿AD翻折△ADC,使点C落在点E,DE交AB于F,若△ADE与△ADB重叠部分面积等于△ABC面积的
,问线段AE与线段BD有什么关系?在图中按要求画出图形,并说明理由.
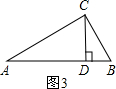
(2)已知:如图3,在△ABC中,∠ACB=90°,AC=2,AB=4,点D是AB边的中点,点P是BC边上的任意一点,连接PD,沿PD翻折△ADP,使点A落在E,若△PDE与△PDB重叠部分的面积等于△ABP面积的
,直接写出BP2的值.
请你直接应用上述结论解决以下问题:

(1)已知:如图2,AD是△ABC的中线,沿AD翻折△ADC,使点C落在点E,DE交AB于F,若△ADE与△ADB重叠部分面积等于△ABC面积的
| 1 |
| 4 |
(2)已知:如图3,在△ABC中,∠ACB=90°,AC=2,AB=4,点D是AB边的中点,点P是BC边上的任意一点,连接PD,沿PD翻折△ADP,使点A落在E,若△PDE与△PDB重叠部分的面积等于△ABP面积的
| 1 |
| 4 |
分析:(1)如图2,线段AE与BD平行且相等;利用上述结论易证得AF=BF,DF=EF;然后通过△AFE≌△BFD(SAS),来证AE=BD,且AE∥BD;
(2)如图3,BP2=4或12.
(2)如图3,BP2=4或12.
解答: (1)解:如图2,线段AE与BD平行且相等.理由如下:
(1)解:如图2,线段AE与BD平行且相等.理由如下:
∵AD是△ABC的中线,
∴S△ABD=S△ADC=
S△ABC.
∵S△ADF=
S△ABC,
∴S△ADF=S△BDF=
S△ABD,
∴AF=BF.
同理,DF=EF.
在△AFE与△BFD中,
,
∴△AFE≌△BFD(SAS),
∴AE=BD,∠EAF=∠DBF,
∴AE∥BD.
∴线段AE与BD平行且相等;
(2)BP2=4或12.
 (1)解:如图2,线段AE与BD平行且相等.理由如下:
(1)解:如图2,线段AE与BD平行且相等.理由如下:∵AD是△ABC的中线,
∴S△ABD=S△ADC=
| 1 |
| 2 |
∵S△ADF=
| 1 |
| 4 |
∴S△ADF=S△BDF=
| 1 |
| 2 |
∴AF=BF.
同理,DF=EF.

在△AFE与△BFD中,
|
∴△AFE≌△BFD(SAS),
∴AE=BD,∠EAF=∠DBF,
∴AE∥BD.
∴线段AE与BD平行且相等;
(2)BP2=4或12.
点评:本题考查了三角形的面积、全等三角形的判定与性质以及翻折变换.折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
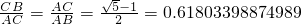 .这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.
.这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.


 .这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.
.这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.


 .这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.
.这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.

