摘要:1.通过复习进一步使学生理解比与比例.线段的比与比例线段.比例中项.比例的基本性质.合比性质.等比性质.进一步使学生理解巩固平行线分线段成比例定理及其推论的图形和结论,三角形一边平行线的性质和判定定理,理解定比分点和黄金分割的概念.
网址:http://m.1010jiajiao.com/timu3_id_443804[举报]
科学研究表明,合理安排各学科的课外学习时间,可以有效的提高学习的效率.教育专家们通过对九年级学生的课外学习时间与学习收益情况进行进一步的研究发现,九年级学生每天课外用于非数学学科的学习时间t(小时)与学习收益量y1的函数关系是图①中的一条折线;每天用于数学学科的学习时间t(小时)与学习收益量y2的函数关系如图②所示:图象中OA是顶点为A的抛物线的一部分,AB是射线.

(1)求出y1与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(2)求出y2与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(3)如果九年级学生每天课外学习的时间为2小时,学习的总收益量为W(W=y1+y2),请问应如何安排学习时间才能使学习的总收益量最大?
查看习题详情和答案>>

(1)求出y1与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(2)求出y2与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(3)如果九年级学生每天课外学习的时间为2小时,学习的总收益量为W(W=y1+y2),请问应如何安排学习时间才能使学习的总收益量最大?
科学研究表明,合理安排各学科的课外学习时间,可以有效的提高学习的效率.教育专家们通过对九年级学生的课外学习时间与学习收益情况进行进一步的研究发现,九年级学生每天课外用于非数学学科的学习时间t(小时)与学习收益量y1的函数关系是图①中的一条折线;每天用于数学学科的学习时间t(小时)与学习收益量y2的函数关系如图②所示:图象中OA是顶点为A的抛物线的一部分,AB是射线.

(1)求出y1与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(2)求出y2与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(3)如果九年级学生每天课外学习的时间为2小时,学习的总收益量为W(W=y1+y2),请问应如何安排学习时间才能使学习的总收益量最大?
查看习题详情和答案>>

(1)求出y1与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(2)求出y2与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(3)如果九年级学生每天课外学习的时间为2小时,学习的总收益量为W(W=y1+y2),请问应如何安排学习时间才能使学习的总收益量最大?
查看习题详情和答案>>
科学研究表明,合理安排各学科的课外学习时间,可以有效的提高学习的效率.教育专家们通过对九年级学生的课外学习时间与学习收益情况进行进一步的研究发现,九年级学生每天课外用于非数学学科的学习时间t(小时)与学习收益量y1的函数关系是图①中的一条折线;每天用于数学学科的学习时间t(小时)与学习收益量y2的函数关系如图②所示:图象中OA是顶点为A的抛物线的一部分,AB是射线.
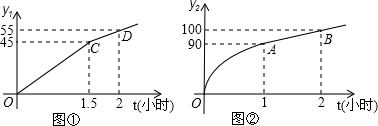
(1)求出y1与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(2)求出y2与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(3)如果九年级学生每天课外学习的时间为2小时,学习的总收益量为W(W=y1+y2),请问应如何安排学习时间才能使学习的总收益量最大?
查看习题详情和答案>>
科学研究表明,合理安排各学科的课外学习时间,可以有效的提高学习的效率.教育专家们通过对九年级学生的课外学习时间与学习收益情况进行进一步的研究发现,九年级学生每天课外用于非数学学科的学习时间t(小时)与学习收益量y1的函数关系是图①中的一条折线;每天用于数学学科的学习时间t(小时)与学习收益量y2的函数关系如图②所示:图象中OA是顶点为A的抛物线的一部分,AB是射线.
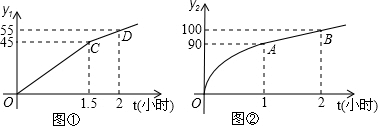
(1)求出y1与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(2)求出y2与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(3)如果九年级学生每天课外学习的时间为2小时,学习的总收益量为W(W=y1+y2),请问应如何安排学习时间才能使学习的总收益量最大?
查看习题详情和答案>>

(1)求出y1与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(2)求出y2与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(3)如果九年级学生每天课外学习的时间为2小时,学习的总收益量为W(W=y1+y2),请问应如何安排学习时间才能使学习的总收益量最大?
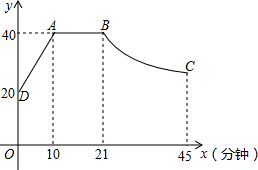 心理学家研究发现,在一节45分钟的课中,学生的注意力随教师讲课的时间的变化而变化,开始学生的注意力逐渐增强,中间学生的注意力保持稳定的状态,随后开始分散,经实验学生的注意力指数y随时间x(分钟)的变化规律如图所示.
心理学家研究发现,在一节45分钟的课中,学生的注意力随教师讲课的时间的变化而变化,开始学生的注意力逐渐增强,中间学生的注意力保持稳定的状态,随后开始分散,经实验学生的注意力指数y随时间x(分钟)的变化规律如图所示.