摘要：25．已知:如图.在平面直角坐标系中.点C在轴上.以C为圆心.4cm为半径的圆与轴相交于点A.B.与轴相交于D.E.且︵AB=︵BD .点P是⊙C上一动点.连结BP.AP. (1)求∠BPA的度数, (2)若过点P的⊙C的切线交轴于点G.是否存在点P.使△APB与以A.G.P为顶点的三角形相似?若存在.求出点P的坐标,若不存在.说明理由.
网址：http://m.1010jiajiao.com/timu3_id_443049[举报]
已知：如图，在平面直角坐标系中，正方形 OABC的顶点B的坐标为（2，2），A、C两点分别在x轴、y轴上．P是BC边上一点（不与B点重合），连AP并延长与x轴交于点E，当点P在边BC上移动时，△AOE的面积随之变化．
①设PB=a（0＜a≤2）．求出△AOE的面积S与a的函数关系式．
②根据①的函数关系式，确定点P在什么位置时，S△AOE=2，并求出此时直线AE的解析式．
③在所给的平面直角坐标系中画出①中函数的图象和函数S=-a+2的简图．
④设函数S=-a+2的图象交a轴于点G，交S轴于点D，点M是①的函数图象上的一动点，过M点向S轴作垂线交函数S=-a+2的图象于点H，过M点向a轴作垂线交函数S=-a+2的图象于点Q，请问DQ•HG的值是否会变化？若不变，
请求出此值；若变化，请说明理由．
查看习题详情和答案>>
①设PB=a（0＜a≤2）．求出△AOE的面积S与a的函数关系式．
②根据①的函数关系式，确定点P在什么位置时，S△AOE=2，并求出此时直线AE的解析式．
③在所给的平面直角坐标系中画出①中函数的图象和函数S=-a+2的简图．
④设函数S=-a+2的图象交a轴于点G，交S轴于点D，点M是①的函数图象上的一动点，过M点向S轴作垂线交函数S=-a+2的图象于点H，过M点向a轴作垂线交函数S=-a+2的图象于点Q，请问DQ•HG的值是否会变化？若不变，
请求出此值；若变化，请说明理由．
查看习题详情和答案>>
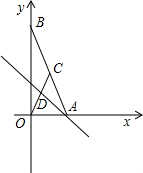已知：如图，在平面直角坐标系中，点A、B分别在x轴、y轴上，线段OA、OB的长（OA＜OB）是方程x2-18x+72=0的两个根，点C是线段AB的中点，点D在线段OC上，且OD=2CD．（1）求点C的坐标；
（2）求直线AD的解析式． 查看习题详情和答案>>
已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A，C的坐标分别为A（-3，0）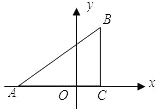
，C（1，0），tan∠BAC=
．
（1）求过点A，B的直线的函数表达式；
（2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；
（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由． 查看习题详情和答案>>
，C（1，0），tan∠BAC=| 3 | 4 |
（1）求过点A，B的直线的函数表达式；
（2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；
（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由． 查看习题详情和答案>>
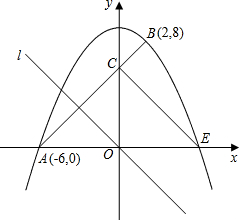和点B（2，8），线段AB交y轴于点C．
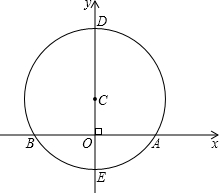与x轴相交于点A、B，与y轴相交于D、E，且