题目内容
已知:如图,在平面直角坐标系中,正方形 OABC的顶点B的坐标为(2,2),A、C两点分别在x轴、y轴上.P是BC边上一点(不与B点重合),连AP并延长与x轴交于点E,当点P在边BC上移动时,△AOE的面积随之变化.①设PB=a(0<a≤2).求出△AOE的面积S与a的函数关系式.
②根据①的函数关系式,确定点P在什么位置时,S△AOE=2,并求出此时直线AE的解析式.
③在所给的平面直角坐标系中画出①中函数的图象和函数S=-a+2的简图.
④设函数S=-a+2的图象交a轴于点G,交S轴于点D,点M是①的函数图象上的一动点,过M点向S轴作垂线交函数S=-a+2的图象于点H,过M点向a轴作垂线交函数S=-a+2的图象于点Q,请问DQ•HG的值是否会变化?若不变,
 请求出此值;若变化,请说明理由.
请求出此值;若变化,请说明理由.
分析:①由相似可以求出OE,△AOE是直角三角形,可以直接求出△AOE的面积.
②把S=2代入得到a=2,PB=2,此时E点与C点重合,求出E点坐标,运用待定系数法求出直线AE的解析式.
③利用描点法画出一次函数和反比例函数的图象.
④通过作辅助线得到△HRG和△DNQ均为等腰直角三角形,利用勾股定理用含a的式子表示出HG、DQ的值,从而求出定值.
②把S=2代入得到a=2,PB=2,此时E点与C点重合,求出E点坐标,运用待定系数法求出直线AE的解析式.
③利用描点法画出一次函数和反比例函数的图象.
④通过作辅助线得到△HRG和△DNQ均为等腰直角三角形,利用勾股定理用含a的式子表示出HG、DQ的值,从而求出定值.
解答:解:①∵B(2,2),且四边形ABCO是正方形.
∴AB=BC=OC=AO=2
∵PB=a
∴PC=2-a
∵△PCE∽△AOE
∴PC:AO=EC:OE
即(2-a):2=(0E-2):OE
解得:OE=
∴S=
(0<a≤2);
②当S=2时,2=
求得:a=2,
∴OE=2,
∴E点C点P点重合.
∴P(2,0)
∴E(2,0),设直线AE的解析式为:y=kx+b则有: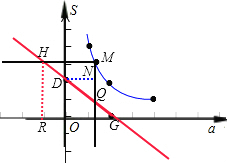
解得:
直线AE的解析式为:y=-x+2;
③作图为:S=
(0<a≤2)与s=-a+2的图象为:
④DQ•HG的值是不会变化的
设M点坐标为(t,
),过H作HR垂直于a轴垂足为R,
过D作DN垂直于MQ垂足为N,易得HR=
,DN=t,
易证△HRG和△DNQ均为等腰直角三角形,由勾股定理得HG=
,DQ=
t
所以DQ•HG=
•
t=8.
∴AB=BC=OC=AO=2
∵PB=a
∴PC=2-a
∵△PCE∽△AOE
∴PC:AO=EC:OE
即(2-a):2=(0E-2):OE
解得:OE=
| 4 |
| a |
∴S=
| 4 |
| a |
②当S=2时,2=
| 4 |
| a |
求得:a=2,
∴OE=2,
∴E点C点P点重合.
∴P(2,0)
∴E(2,0),设直线AE的解析式为:y=kx+b则有:

|
|
直线AE的解析式为:y=-x+2;
③作图为:S=
| 4 |
| a |
④DQ•HG的值是不会变化的
设M点坐标为(t,
| 4 |
| t |
过D作DN垂直于MQ垂足为N,易得HR=
| 4 |
| t |
易证△HRG和△DNQ均为等腰直角三角形,由勾股定理得HG=
4
| ||
| t |
| 2 |
所以DQ•HG=
4
| ||
| t |
| 2 |
点评:本题是一道一次函数和反比例函数的综合试题,考查了待定系数法求函数的解析式,描点法画函数图象、等腰直角三角形的性质以及勾股定理的运用等多个知识点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).

