摘要:14.已知抛物线的图象与轴有两个交点.那么一元二次方程的根的情况是 ,
网址:http://m.1010jiajiao.com/timu3_id_442631[举报]
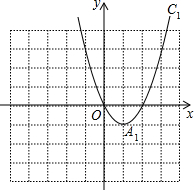 已知抛物线C1:y=x2-2x的图象如图所示,把C1的图象沿y轴翻折,得到抛物线C2的图象,抛物线C1与抛物线C2的图象合称图象C3.
已知抛物线C1:y=x2-2x的图象如图所示,把C1的图象沿y轴翻折,得到抛物线C2的图象,抛物线C1与抛物线C2的图象合称图象C3.(1)求抛物线C1的顶点A坐标,并画出抛物线C2的图象;
(2)若直线y=kx+b与抛物线y=ax2+bx+c(a≠0)有且只有一个交点时,称直线与抛物线相切.若直线y=x+b与抛物线C1相切,求b的值;
(3)结合图象回答,当直线y=x+b与图象C3有两个交点时,b的取值范围. 查看习题详情和答案>>
已知抛物线y=ax2+bx-4的图象与x相交于A、B(点A在B的左边),与y轴相交于C,抛物线过点A(-1,0)且OB=OC.P是线段BC上的一个动点,过P作直线PE⊥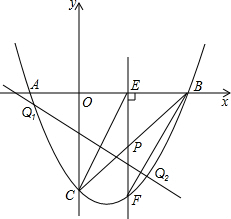 x轴于E,交抛物线于F.
x轴于E,交抛物线于F.
(1)求抛物线的解析式;
(2)若△BPE与△BPF的两面积之比为2:3时,求E点的坐标;
(3)设OE=t,△CPE的面积为S,试求出S与t的函数关系式;当t为何值时,S有最大值,并求出最大值;
(4)在(3)中,当S取得最大值时,在抛物线上求点Q,使得△QEC是以EC为底边的等腰三角形,求Q的坐标. 查看习题详情和答案>>
 x轴于E,交抛物线于F.
x轴于E,交抛物线于F.(1)求抛物线的解析式;
(2)若△BPE与△BPF的两面积之比为2:3时,求E点的坐标;
(3)设OE=t,△CPE的面积为S,试求出S与t的函数关系式;当t为何值时,S有最大值,并求出最大值;
(4)在(3)中,当S取得最大值时,在抛物线上求点Q,使得△QEC是以EC为底边的等腰三角形,求Q的坐标. 查看习题详情和答案>>
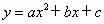 的图象与x轴有两个交点,那么一元二次方程
的图象与x轴有两个交点,那么一元二次方程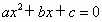 的根的情况是________.
的根的情况是________.