题目内容
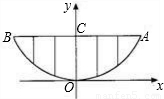
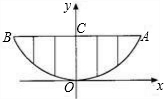 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米,以O为原点,OC所在的直线为y轴建立平面直角坐标系,根据以上的数据,则这段栅栏所需立柱的总长度(精确到0.1米)为( )
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米,以O为原点,OC所在的直线为y轴建立平面直角坐标系,根据以上的数据,则这段栅栏所需立柱的总长度(精确到0.1米)为( )| A、1.5米 | B、1.9米 | C、2.3米 | D、2.5米 |
分析:由题意可知,A点坐标为(0.6,0.6),代入y=ax2,可求出解析式.由于OC左右两边四根栅栏的底端横坐标已知,根据所求解析式,可计算出纵坐标,高度也就可以表示出来,计算即可.
解答:解:抛物线顶点在原点,
设抛物线解析式为y=ax2,
把点A(0.6,0.6)代入解析式得a=
,
∴y=
x2
∴(0.2,
),(0.4,
)是该抛物线的两点,
∴这段栅栏所需立柱的总长度=(0.6-
+0.6-
)×2+0.6≈2.3米.
故选C.
设抛物线解析式为y=ax2,
把点A(0.6,0.6)代入解析式得a=
| 5 |
| 3 |
∴y=
| 5 |
| 3 |
∴(0.2,
| 1 |
| 15 |
| 4 |
| 15 |
∴这段栅栏所需立柱的总长度=(0.6-
| 1 |
| 15 |
| 4 |
| 15 |
故选C.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.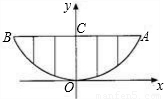 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.