摘要： 已知.如图.直角坐标系内的矩形ABCD.顶点A的坐标为(0.3).BC＝2AB.P为AD边上一动点.以点P为圆心作⊙P与对角线AC相切于点F.过P.F作直线L.交BC边于点E .当点P运动到点P1位置时.直线L恰好经过点B.此时直线的解析式是y＝2x+1 ⑴求BC.AP1的长, ⑵设AP＝m.梯形PECD的面积为S.求S与m之间的函数关系式.写出自变量m的取值范围, ⑶以点E为圆心作⊙E与x轴相切 ①探究并猜想:⊙P和⊙E有哪几种位置关系.并求出AP相应的取值范围, ②当直线L把矩形ABCD分成两部分的面积之比值为3∶5时.则⊙P和⊙E的位置关系如何?并说明理由.
网址：http://m.1010jiajiao.com/timu3_id_440457[举报]
（本小题10分）在等腰梯形ABCD中，AD∥BC，且AD=2，以CD为直径作⊙
O1，交BC于点E，过点E作EF⊥AB于F，建立如图12所示的平面直角坐标系，已知A，
B两点的坐标分别为A(0，2
)，B(-2，0).
（1）求C，D两点的坐标.
（2）求证：EF为⊙O1的切线.
（3）探究：如图13，线段CD上是否存在点P，使得线段PC的长度与P点到y轴的距离相等？如果存在，请找出P点的坐标；如果不存在，请说明理由.
查看习题详情和答案>>
（本小题10分）在等腰梯形ABCD中，AD∥BC，且AD=2，以CD为直径作⊙
O1，交BC于点E，过点E作EF⊥AB于F，建立如图12所示的平面直角坐标系，已知A，
B两点的坐标分别为A(0，2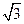
)，B(-2，0).
（1）求C，D两点的坐标.
（2）求证：EF为⊙O1的切线.
（3）探究：如图13，线段CD上是否存在点P，使得线段PC的长度与P点到y轴的距离相等？如果存在，请找出P点的坐标；如果不存在，请说明理由.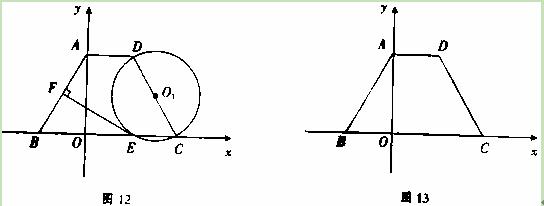
查看习题详情和答案>>
O1，交BC于点E，过点E作EF⊥AB于F，建立如图12所示的平面直角坐标系，已知A，
B两点的坐标分别为A(0，2
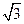)，B(-2，0).（1）求C，D两点的坐标.
（2）求证：EF为⊙O1的切线.
（3）探究：如图13，线段CD上是否存在点P，使得线段PC的长度与P点到y轴的距离相等？如果存在，请找出P点的坐标；如果不存在，请说明理由.
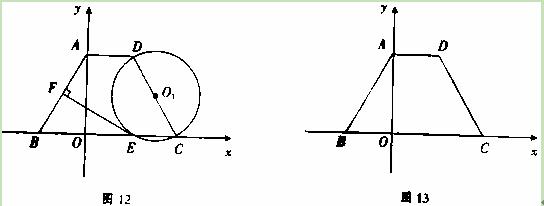查看习题详情和答案>>
（本小题10分）在等腰梯形ABCD中，AD∥BC，且AD=2，以CD为直径作⊙
O1，交BC于点E，过点E作EF⊥AB于F，建立如图12所示的平面直角坐标系，已知A，
B两点的坐标分别为A(0，2
)，B(-2，0).
（1）求C，D两点的坐标.
（2）求证：EF为⊙O1的切线.
（3）探究：如图13，线段CD上是否存在点P，使得线段PC的长度与P点到y轴的距离相等？如果存在，请找出P点的坐标；如果不存在，请说明理由.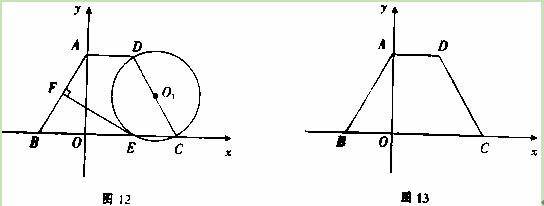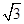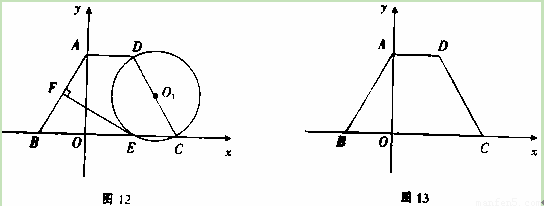
)，B(-2，0).
)，B(-2，0).