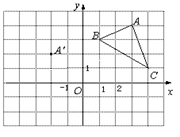
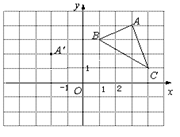
摘要： 如图1所示.平面直角坐标系中有一张矩形纸片OABC.O为坐标原点.A点坐标为.D是BC边上的动点.现将△COD沿OD翻折.得到△FOD,再在AB边上选取适当的点E.将△BDE沿DE翻折.得到△GDE.并使直线DG.DF重合. 图1 (1)如图2所示.若翻折后点F落在OA边上.求直线DE的函数关系式, 图2 .求b关于a的函数关系式.并求b的最小值, (3)一般地.请你猜想直线DE与抛物线的公共点的个数.在图2的情形中通过计算验证你的猜想,如果直线DE与抛物线始终有公共点.请在图1中作出这样的公共点. [试题答案]
网址：http://m.1010jiajiao.com/timu3_id_440309[举报]
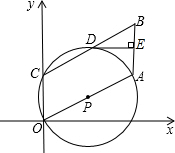在如图所示的平面直角坐标系中，点C在y轴的正半轴上，四边形OABC为平行四边形，OA=2，∠AOC=60°，以OA为直径的⊙P经过点C，交BC于点D，DE⊥AB，交AB于E．（1）求点A和B的坐标；
（2）求证：DE是⊙P的切线；
（3）小明在解答本题时，发现连结DA并延长，交x轴于点N，则△AON是等腰三角形．由此，他断定：“x轴上一定存在除点N以外的点Q，使△AOQ也是等腰三角形，且点Q一定在⊙P外”．你同意他的看法吗？请充分说明理由．
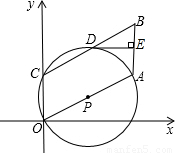
在如图所示的平面直角坐标系中，点C在y轴的正半轴上，四边形OABC为平行四边形，OA=2，∠AOC=60°，以OA为直径的⊙P经过点C，交BC于点D，DE⊥AB，交AB于E．
（1）求点A和B的坐标；
（2）求证：DE是⊙P的切线；
（3）小明在解答本题时，发现连结DA并延长，交x轴于点N，则△AON是等腰三角形．由此，他断定：“x轴上一定存在除点N以外的点Q，使△AOQ也是等腰三角形，且点Q一定在⊙P外”．你同意他的看法吗？请充分说明理由．
查看习题详情和答案>>
（1）求点A和B的坐标；
（2）求证：DE是⊙P的切线；
（3）小明在解答本题时，发现连结DA并延长，交x轴于点N，则△AON是等腰三角形．由此，他断定：“x轴上一定存在除点N以外的点Q，使△AOQ也是等腰三角形，且点Q一定在⊙P外”．你同意他的看法吗？请充分说明理由．
查看习题详情和答案>>
如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙
交x轴于D点，过点D作DF⊥AE于点F．
(1)求OA、OC的长；
(2)求证：DF为⊙的切线；
(3)小明在解答本题时，发现△AOE是等腰三角形．
他与同学小刚一起研究：“直线BC上除点E以外还存在其它点P，使△AOP也是等腰三角形吗？”结果发现还有其它点．小明说：点P一定在⊙外．你同意他的看法吗？请充分说明理由．并把所有满足条件的点的坐标表示出来．
