摘要： 已知.如图.在直角梯形ABCD.AD∥ BC.BC=5cm.CD=6cm.∠DCB=60O.∠ABC=90O.等边三角形△MPN的边长为acm.边MN和直角梯形ABCD的底边BC都在直线 上.NC=8cm.将直角梯形ABCD向左翻折180O.翻折一次得到图形①.翻折二次得到图形②.如此翻折下去. (1) 将直角梯形ABCD向左翻折二次.如果此时等边三角形的边长a≥2cm.这时两图形重叠部分的面积是多少? (2) 将直角梯形ABCD向左翻折三次.如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积.这时等边三角形的边长a至少应为多少 ? (3) 将直角梯形ABCD向左翻折三次.如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积的一半.这时等边三角形的边长a 应为多少 ?
网址：http://m.1010jiajiao.com/timu3_id_440037[举报]
（本题12分）已知两个全等的直角三角形纸片ABC、DEF，如图（1）放置，点B、D重合，点F在BC上，AB与EF交于点G，∠C＝∠EFB＝90°，∠E＝∠ABC＝30°，AB＝DE＝4.
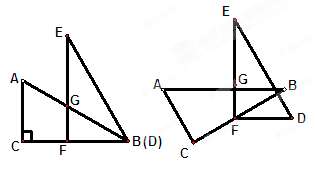
1.（1）求证：△EGB是等腰三角形
2.（2）若纸片DEF不动，问△ABC绕点F逆时针旋转最小 度时，四边形ACDE成为以ED为底的梯形（如图（2）），求此梯形的高。
查看习题详情和答案>>
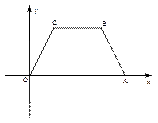
(本题12分)如图，在平面直角坐标系中，等腰梯形OABC，CB//OA，且点A在x轴正半轴上.已知C(2，4)，BC=4.
(1)求过O、C、B三点的抛物线解析式，并写出顶点坐标和对称轴；
(2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合)，使得P点到两坐标轴的
距离相等.如果存在，求出P点坐标；如果不存在，请说明理由.
查看习题详情和答案>>
(本题12分)如图，在平面直角坐标系中，等腰梯形OABC，CB//OA，且点A在x轴正半轴上.已知C(2，4)，BC= 4.
(1)求过O、C、B三点的抛物线解析式，并写出顶点坐标和对称轴；
(2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合)，使得P点到两坐标轴的
距离相等.如果存在，求出P点坐标；如果不存在，请说明理由.
查看习题详情和答案>>
(1)求过O、C、B三点的抛物线解析式，并写出顶点坐标和对称轴；
(2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合)，使得P点到两坐标轴的
距离相等.如果存在，求出P点坐标；如果不存在，请说明理由.
查看习题详情和答案>>
