摘要:2.为配和新课程的实施.某市举行了“应用与创新 知识竞赛.共有1万名学生参加了这次竞赛(满分100分.得分全为整数).为了解本次竞赛成绩情况.从中随机抽取了部分学生的竞赛成绩.进行统计.整理见下表: 组别 分 组 频 数 频率 1 49.5-59.5 60 0.12 2 59.5-69.5 120 0.24 3 69.5-79.5 180 0.36 4 79.5-89.5 130 5 89.5-99.5 0.02 合 计 1.00 解答下列问题: (1)在这个问题中.总体是 .样本容量= , (2)第四小组的频率= , (3)被抽取的学生成绩的中位数落在第几小组内? (4)若成绩在90分以上的学生获一等奖.请你估计全市获一等奖的人数. 资阳 甲.乙两同学开展“投球进筐 比赛.双方约定:① 比赛分6局进行.每局在指定区域内将球投向筐中.只要投进一次后该局便结束,② 若一次未进可再投第二次.以此类推.但每局最多只能投8次.若8次投球都未进.该局也结束,③ 计分规则如下:a. 得分为正数或0,b. 若8次都未投进.该局得分为0,c. 投球次数越多.得分越低,d. 6局比赛的总得分高者获胜 . (1) 设某局比赛第n(n=1,2,3,4,5,6,7,8)次将球投进.请你按上述约定.用公式.表格或语言叙述等方式.为甲.乙两位同学制定一个把n换算为得分M的计分方案, (2) 若两人6局比赛的投球情况如下(其中的数字表示该局比赛进球时的投球次数.“× 表示该局比赛8次投球都未进): 第一局 第二局 第三局 第四局 第五局 第六局 甲 5 × 4 8 1 3 乙 8 2 4 2 6 × 根据上述计分规则和你制定的计分方案.确定两人谁在这次比赛中获胜. (1)计分方案如下表: n(次) 1 2 3 4 5 6 7 8 M(分) 8 7 6 5 4 3 2 1 (用公式或语言表述正确.同样给分.) (2) 根据以上方案计算得6局比赛.甲共得24分.乙共得分23分. 所以甲在这次比赛中获胜 06年模拟 如下图是9×7的正方形点阵.其水平方向和竖起直方向的两格点间的长度都为1个单位.以这些点为顶点的三角形称为网格三角形.请通过画图分析.探究回答下列问题: (1)请在图中画出以AB为边且面积为2的一个网格三角形, (2)任取该网格中的一点M.求以A.B.M为顶点的三角形的面积为2的概率, (3)任取该网格中的一点M.求以A.B.M为顶点的三角形为直角三角形的概率,
网址:http://m.1010jiajiao.com/timu3_id_439724[举报]
24、为配和新课程的实施,某市举行了“应用与创新”知识竞赛,共有1万名学生参加了这次竞赛(满分100分,得分全为整数).为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
解答下列问题:
(1)在这个问题中,总体是
(2)第四小组的频率c=
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计全市获一等奖的人数.
查看习题详情和答案>>
| 组别 | 分组 | 频数 | 频率 |
| 1 | 49.5~59.5 | 60 | 0.12 |
| 2 | 59.5~69.5 | 120 | 0.24 |
| 3 | 69.5~79.5 | 180 | 0.36 |
| 4 | 79.5~89.5 | 130 | c |
| 5 | 89.5~99.5 | b | 0.02 |
| 合计 | a | 1.00 | |
(1)在这个问题中,总体是
1万名学生的竞赛成绩
,样本容量a=500
;(2)第四小组的频率c=
0.26
;(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计全市获一等奖的人数.
11、为配和新课程的实施,某市举行了“应用与创新”知识竞赛,共有1万名学生参加了这次竞赛(满分100分,得分全为整数).为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
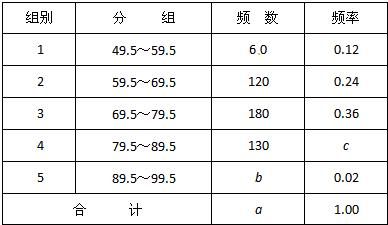
表中a=
查看习题详情和答案>>

表中a=
500
,b=10
,c=0.26
;若成绩在90分以上(含90分)的学生获一等奖,估计全市获一等奖的人数为200
.为配和新课程的实施,某市举行了“应用与创新”知识竞赛,共有1万名学生参加了这次竞赛(满分100分,得分全为整数).为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
| 组别 | 分组 | 频数 | 频率 |
| 1 | 49.5~59.5 | 60 | 0.12 |
| 2 | 59.5~69.5 | 120 | 0.24 |
| 3 | 69.5~79.5 | 180 | 0.36 |
| 4 | 79.5~89.5 | 130 | c |
| 5 | 89.5~99.5 | b | 0.02 |
| 合计 | a | 1.00 | |
(1)在这个问题中,总体是______,样本容量a=______;
(2)第四小组的频率c=______;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计全市获一等奖的人数. 查看习题详情和答案>>
为配和新课程的实施,某市举行了“应用与创新”知识竞赛,共有1万名学生参加了这次竞赛(满分100分,得分全为整数).为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
解答下列问题:
(1)在这个问题中,总体是______,样本容量a=______;
(2)第四小组的频率c=______;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计全市获一等奖的人数.
查看习题详情和答案>>
| 组别 | 分组 | 频数 | 频率 |
| 1 | 49.5~59.5 | 60 | 0.12 |
| 2 | 59.5~69.5 | 120 | 0.24 |
| 3 | 69.5~79.5 | 180 | 0.36 |
| 4 | 79.5~89.5 | 130 | c |
| 5 | 89.5~99.5 | b | 0.02 |
| 合计 | a | 1.00 | |
(1)在这个问题中,总体是______,样本容量a=______;
(2)第四小组的频率c=______;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计全市获一等奖的人数.
为配和新课程的实施,某市举行了“应用与创新”知识竞赛,共有1万名学生参加了这次竞赛(满分100分,得分全为整数).为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
表中a=______,b=______,c=______;若成绩在90分以上(含90分)的学生获一等奖,估计全市获一等奖的人数为______.
查看习题详情和答案>>
| 组别 | 分组 | 频数 | 频率 |
| 1 | 49.5~59.5 | 6.0 | 0.12 |
| 2 | 59.5~69.5 | 120 | 0.24 |
| 3 | 69.5~79.5 | 180 | 0.36 |
| 4 | 79.5~89.5 | 130 | c |
| 5 | 89.5~99.5 | b | 0.02 |
| 合计 | a | 1.00 |