摘要：已知在Rt△ABC中∠ABC＝90°.D为AC上一点.且AD和CD的长是关于X的一元二次方程x2-12x+m2+4m+40＝0的两个实数根.⊙O经过A.D.B三点.CB的延长线交⊙O于点E.过点E作⊙O的切线交AC延长线于点F.连续DE交AB于N.连接ON和CN. (1)求证:△ABD为等腰三角形; (2)过D作DM⊥AE于M.若满足CF·DE＝AE·DM.求sin∠FAB的值; 条件下.求作以NO.NC为根的一元二方程.
网址：http://m.1010jiajiao.com/timu3_id_439701[举报]
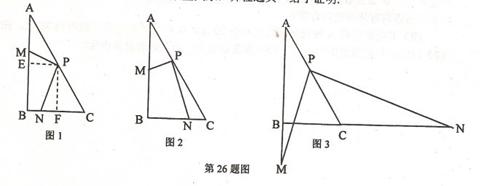
已知在Rt△ABC中，∠A
BC＝90º，∠A＝30º，点P在AC上，且∠MPN＝90º．
当点P为线段AC的中点，点M、N分别在线段AB、BC上时（如图1），过点P作PE⊥AB于点E，PF⊥BC于点F，可证t△PME∽t△PNF，得出PN＝
PM．（不需证明）
当PC＝
PA，点M、N分别在线段AB、BC或其延长线上，如图2、图3这两种情况时，请写出线段PN、PM之间的数量关系，并任选取一给予证明．
已知在Rt△ABC中，∠ABC＝90°，∠A＝30°，点P在AC上，且∠MPN＝90°．
当点P为线段AC的中点，点M、N分别在线段AB、BC上时(如图1)，过点P作PE⊥AB于点E，PF⊥BC于点F，可证t△PME∽t△PNF，得出PN＝
PM．
(不需证明)
当PC＝
PA，点M、N分别在线段AB、BC或其延长线上，如图2、图3这两种情况时，请写出线段PN、PM之间的数量关系，并任选取一给予证明．
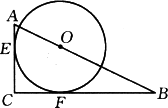
已知：在Rt△ABC中，∠C＝90°，O为斜边AB上的一点，以O为圆心的圆与边AC、BC分别相切于点E、F，若AC＝1，BC＝3，则⊙O的半径为
[ ]
A．
B．
C．
D．
．