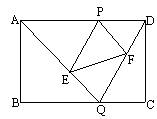
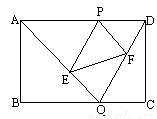
摘要：如图.已知矩形ABCD的边长AB=2.BC=3.点P是AD边上的一动点.Q是BC边上的任意一点. 连AQ.DQ.过P作PE∥DQ交AQ于E.作PF∥AQ交DQ于F. (1)求证:△APE∽△ADQ, (2)设AP的长为x.试求△PEF的面积S△PEF关于x的函数关系式.并求当P在何处时.S△PEF取得最大值?最大值为多少? (3)当Q在何处时.△ADQ的周长最小?(须给出确定Q在何处的过程或方法.不必给出证明)
网址：http://m.1010jiajiao.com/timu3_id_439474[举报]
如图，已知矩形ABCD的边长AB=3cm，BC=6cm，某一时刻，动点M从点A出发沿AB方向以1cm∕s的速度向点B匀速运动；同时，动点N从点D沿DA方向以2cm∕s的速度向点A匀速运动．经过多少时间，△AMN的面积等于矩形ABCD面积的| 1 | 9 |
如图，已知矩形ABCD的边长AB=3cm，BC=6cm，某一时刻，动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动；同时，动点N从点D沿DA方向以2cm/s的速度向点A匀速运动．（1）经过多少时间，△AMN的面积等于矩形ABCD面积的
| 1 | 9 |
（2）是否存在时刻t，使A、M、N为顶点的三角形与△ACD相似？若存在，求t的值；若不存在，请说明理由．
如图，已知矩形ABCD的边长AB=2，BC=3，点Q是BC边的中点，点P是AD边上的一个动点，PE∥DQ交AQ于点E，PF∥AQ交DQ于点F．（1）四边形PEQF的形状是
平行四边形
平行四边形
．（2）当P运动到什么位置时，四边形PEQF是菱形？并说明理由．
（3）四边形PEQF
不可能
不可能
为正方形（填“可能”或“不可能”）．
