摘要:已知⊙O内两弦AB.CD相交于E , E是弦AB的中点.CE = 4cm .DE = 9cm .OE = 8cm .则⊙O的直径等于___
网址:http://m.1010jiajiao.com/timu3_id_439237[举报]
请阅读下列材料:
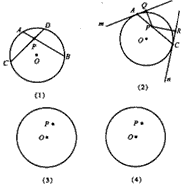
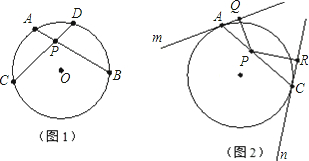
圆内的两条相交弦,被交点分成的两条线段长的积相等,即如图(1),若弦AB、CD交于点P则PA·PB=PC·PD,请你根据以上材料,解决下列问题,已知⊙O的半径为2,P是⊙O内一点,且OP=1,过点P任作一弦AC,过A、C两点分别作圆O的切线m和n,作PQ⊥m于点Q,PR⊥n于点R。(如图(2))
圆内的两条相交弦,被交点分成的两条线段长的积相等,即如图(1),若弦AB、CD交于点P则PA·PB=PC·PD,请你根据以上材料,解决下列问题,已知⊙O的半径为2,P是⊙O内一点,且OP=1,过点P任作一弦AC,过A、C两点分别作圆O的切线m和n,作PQ⊥m于点Q,PR⊥n于点R。(如图(2))
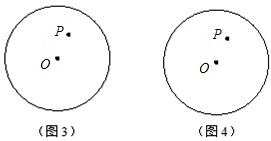
(1)若AC恰经过圆心O,请你在图(3)中画出符合题意的图形,并计算: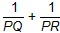 的值;
的值;
(2)若OP⊥AC,请你在图(4)中画出符合题意的图形,并计算: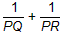 的值;
的值;
(3)若AC是过点P的任一弦(图(2)),请你结合(1)(2)的结论,猜想: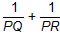 的值,并给出证明。
的值,并给出证明。
查看习题详情和答案>>
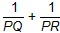 的值;
的值;(2)若OP⊥AC,请你在图(4)中画出符合题意的图形,并计算:
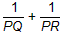 的值;
的值;(3)若AC是过点P的任一弦(图(2)),请你结合(1)(2)的结论,猜想:
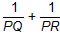 的值,并给出证明。
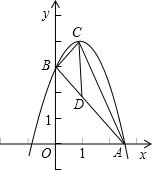
的值,并给出证明。(1)如图,AB、CD是⊙O的两条弦,它们相交于点P,连接AD、BD,已知AD=BD=4,PC=6,那么CD的长是______.
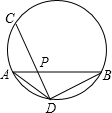
(2)阅读材料:如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法: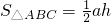 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
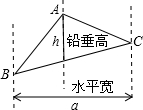
如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
①求抛物线和直线AB的解析式;
②点P是抛物线(在第一象限内)上的一个动点,连接PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;
③点P是抛物线(在第一象限内)上的一个动点,是否存在一点P,使S△PAB= S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
查看习题详情和答案>>
附加题:
(1)如图,AB、CD是⊙O的两条弦,它们相交于点P,连接AD、BD,已知AD=BD=4,PC=6,那么CD的长是 .
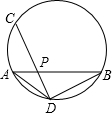
(2)阅读材料:如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:S△ABC=
ah,即三角形面积等于水平宽与铅垂高乘积的一半.

解答下列问题:
如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
①求抛物线和直线AB的解析式;
②点P是抛物线(在第一象限内)上的一个动点,连接PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;
③点P是抛物线(在第一象限内)上的一个动点,是否存在一点P,使S△PAB=
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)如图,AB、CD是⊙O的两条弦,它们相交于点P,连接AD、BD,已知AD=BD=4,PC=6,那么CD的长是

(2)阅读材料:如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:S△ABC=
| 1 |
| 2 |

解答下列问题:
如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
①求抛物线和直线AB的解析式;
②点P是抛物线(在第一象限内)上的一个动点,连接PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;
③点P是抛物线(在第一象限内)上的一个动点,是否存在一点P,使S△PAB=
| 9 |
| 8 |
 查看习题详情和答案>>
查看习题详情和答案>>
附加题:
(1)如图,AB、CD是⊙O的两条弦,它们相交于点P,连接AD、BD,已知AD=BD=4,PC=6,那么CD的长是______.
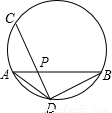
(2)阅读材料:如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法: ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.

解答下列问题:
如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
①求抛物线和直线AB的解析式;
②点P是抛物线(在第一象限内)上的一个动点,连接PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;
③点P是抛物线(在第一象限内)上的一个动点,是否存在一点P,使S△PAB= S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.

查看习题详情和答案>>
(1)如图,AB、CD是⊙O的两条弦,它们相交于点P,连接AD、BD,已知AD=BD=4,PC=6,那么CD的长是______.

(2)阅读材料:如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:
 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
①求抛物线和直线AB的解析式;
②点P是抛物线(在第一象限内)上的一个动点,连接PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;
③点P是抛物线(在第一象限内)上的一个动点,是否存在一点P,使S△PAB=
 S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
查看习题详情和答案>>
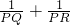 的值;
的值;