摘要：关于 x 的方程 x2 + b2 =2 (A) (B) (C) (D)

网址：http://m.1010jiajiao.com/timu3_id_439087[举报]

（1）解方程求出两个解x₁、x₂，并计算两个解的和与积，填人下表

x₁

x₂

关于x的方程ax²+bx+c=0
（a、b、c为常数，
且a≠0，b²-4ac≥0）

（2）观察表格中方程两个解的和、两个解的积与原方程的系数之间的关系有什么规律？写出你的结论．查看习题详情和答案>>

阅读材料关于x的方程ax²+bx+c=0（a、b、c为常数，且a≠0，b²-4ac≥0）
的两根为x₁=

，则我们通过计算可得：x1+x2=

即：若x₁和x₂是方程ax²+bx+c=0（a≠0）的两个根，那么x1+x2=-

．
解决问题：
（1）若x₁和x₂是方程2x²-3x-6=0的两个根，求x₁²x₂+x₁x₂²的值．
（2）若x₁和x₂是方程2x²+4x+m=0的两个根，求x₁²+x₂²的最小值．查看习题详情和答案>>

（1）解方程求出两个解x₁、x₂，并计算两个解的和与积，填人下表
方程 x₁ x₂ x₁+x₂ x₁•x₂
9x²-2=0
2x²-3x=0
x²-3x+2=0
关于x的方程ax²+bx+c=0
（a、b、c为常数，
且a≠0，b²-4ac≥0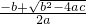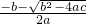） $数学公式$ $数学公式$
（2）观察表格中方程两个解的和、两个解的积与原方程的系数之间的关系有什么规律？写出你的结论．

查看习题详情和答案>>

（1）解方程求出两个解x₁，x₂，并计算两个解的和与积，填入下表：
方程 x₁ x₂ x₁+x₂ x₁•x₂
x²-5x+4=0
4x²-8x-5=0
关于x的方程ax²+bx+c=0（a，b
，c为常数，且a≠0，b²-4ac≥0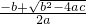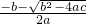） $数学公式$ $数学公式$
（2）观察表格中方程两个解的和、两个解的积与原方程的系数之间的关系有什么规律？写出你的结论；
（3）已知x₁、x₂是方程2x²-4x+1=0的两个根，不解方程，利用（2）中的结论，求 $数学公式$ 的值．

查看习题详情和答案>>

阅读材料关于x的方程ax²+bx+c=0（a、b、c为常数，且a≠0，b²-4ac≥0）
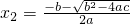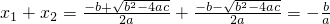
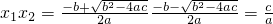
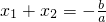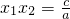的两根为x₁= $数学公式$ $数学公式$ ，则我们通过计算可得： $数学公式$ $数学公式$
即：若x₁和x₂是方程ax²+bx+c=0（a≠0）的两个根，那么 $数学公式$ ， $数学公式$ ．
解决问题：
（1）若x₁和x₂是方程2x²-3x-6=0的两个根，求x₁²x₂+x₁x₂²的值．
（2）若x₁和x₂是方程2x²+4x+m=0的两个根，求x₁²+x₂²的最小值．

查看习题详情和答案>>