题目内容
阅读材料关于x的方程ax2+bx+c=0(a、b、c为常数,且a≠0,b2-4ac≥0)的两根为x1=
-b+
| ||
| 2a |
-b-
| ||
| 2a |
-b+
| ||
| 2a |
-b-
| ||
| 2a |
| b |
| a |
-b+
| ||
| 2a |
-b-
| ||
| 2a |
| c |
| a |
即:若x1和x2是方程ax2+bx+c=0(a≠0)的两个根,那么x1+x2=-
| b |
| a |
| c |
| a |
解决问题:
(1)若x1和x2是方程2x2-3x-6=0的两个根,求x12x2+x1x22的值.
(2)若x1和x2是方程2x2+4x+m=0的两个根,求x12+x22的最小值.
分析:(1)把所求式子进行因式分解,再利用根与系数的关系求则可.
(2)把所求式子整理为两根之和与两根之积的形式,代入数值,再讨论式子的最小值.
(2)把所求式子整理为两根之和与两根之积的形式,代入数值,再讨论式子的最小值.
解答:解:(1)由题可知x1+x2=-
=
,x1•x2=
=-3,
∴
x2+x1
=x1x2(x1+x2)=
×(-3)=-
,
(2)由题可知x1+x2=-
=-2,x1•x2=
,
∴
+
=(x1+x2)2-2x1x2=(-2)2-2×
=4-m,
∵b2-4ac≥0即42-4×2×m≥0,解得m≤2,
∴当m=2时,x12+x22的最小值为4-2=2.
| -3 |
| 2 |
| 3 |
| 2 |
| -6 |
| 2 |
∴
| x | 2 1 |
| x | 2 2 |
| 3 |
| 2 |
| 9 |
| 2 |
(2)由题可知x1+x2=-
| 4 |
| 2 |
| m |
| 2 |
∴
| x | 2 1 |
| x | 2 2 |
| m |
| 2 |
∵b2-4ac≥0即42-4×2×m≥0,解得m≤2,
∴当m=2时,x12+x22的最小值为4-2=2.
点评:本题考查了一元二次方程根与系数的关系及根的判别式,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法,需注意运用根的判别式求出m的取值范围.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
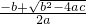
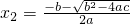 ,则我们通过计算可得:
,则我们通过计算可得: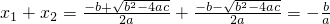
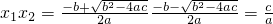
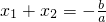 ,
,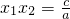 .
.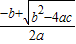
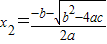 ,则我们通过计算可得:
,则我们通过计算可得: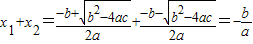
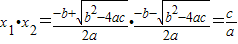
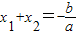 ,
,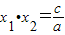 .
.