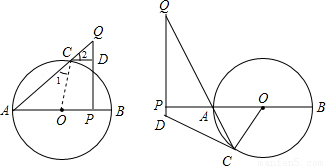
摘要：对上述命题证明如下: 证明:连结OC ∵OA＝OC ∴∠A＝∠1 ∵CD切O于C点 ∴∠OCD＝90° ∴∠1+∠2＝90° ∴∠A+∠2＝90° 在RtQPA中.QPA＝90° ∴∠A+∠Q＝90° ∴∠2＝∠Q ∴DQ＝DC 即CDQ是等腰三角形. 问题:对上述命题.当点P在BA的延长线上时.其他条件不变.如图9所示.结论“△CDQ是等腰三角形 还成立吗?若成立.误给予证明,若不成立.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_438200[举报]
利用切线性质证明等腰三角形
如图，已知：如图(1)，AB是⊙O的直径，P是AB上的一点(与A、B不重合)．QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D，则△CDQ是等腰三角形．对上述命题证明如下：
证明：连结OC．
∵OA＝OC，∴∠A＝∠1．
∵CD切⊙O于C点，
∴∠OCD＝90°，
∴∠1＋∠2＝90°，
∴∠A＋∠2＝90°．
在Rt△QPA中，∠QPA＝90°，
∴∠A＋∠Q＝90°，
∴∠2＝∠Q．∴DQ＝DC．
即△CDQ是等腰三角形．
问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图(2)所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．
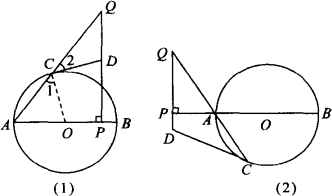
如图，AB是⊙
的直径，P是AB上一点(与点A，B不重合)，QP⊥AB，垂足为P点，直线QA交⊙于C点，过点C作⊙的切线交直线QP于点D．则△CDQ是等腰三角形．对上述命题证明如下：
证明：连接OC．
∵OA=OC，∴∠A=∠1．
∵CD切⊙于C点，
∴∠OCD=90°，∴∠1+∠2=90°，∴∠A+∠2=90°．
在Rt△QPA中，∠QPA=90°，
∴∠A+∠Q=90°，∴∠2=∠Q，∴DQ=DC．
即△CDQ是等腰三角形．
问题：对上述命题，当点P在BA的延长线上时，其他条件不变．
如图所示，结论“△CDQ是等腰三角形”还成立吗?若成立，请给予证明；若不成立，请说明理由．
20、已知：如图，AB是⊙O的直径，P是AB上的一点（与A、B不重合），QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D．则△CDQ是等腰三角形．
对上述命题证明如下：
证明：连接OC
∵OA=OC
∴∠A=∠1
∵CD切O于C点
∴∠OCD=90°
∴∠1+∠2=90°
∴∠A+∠2=90°
在RtQPA中，∠QPA=90°
∴∠A+∠Q=90°
∴∠2=∠Q
∴DQ=DC
即CDQ是等腰三角形．
问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．
查看习题详情和答案>>
对上述命题证明如下：证明：连接OC
∵OA=OC
∴∠A=∠1
∵CD切O于C点
∴∠OCD=90°
∴∠1+∠2=90°
∴∠A+∠2=90°
在RtQPA中，∠QPA=90°
∴∠A+∠Q=90°
∴∠2=∠Q
∴DQ=DC
即CDQ是等腰三角形．
问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．
