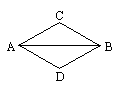
摘要: 证: ⑴∵AD∥BC ∴AD∥CE 又∵DE∥AC ∴四边形ACED是平行四边形------ 4分 ⑵过D点作DF⊥BE于F点 --------5分 ∵DE∥AC.AC⊥BD ∴DE⊥BD.即∠BDE=90°--------6分 由⑴知DE=AC.CE=AD=3 ∵四边形ABCD是等腰梯形 ∴AC=DB----7分 ∴DE=DB ------------8分 ∴△DBE是等腰直角三角形.∴△DFB也是等腰直角三角形 ∴DF=BF=(7-3)+3=5--------10分 (也可运用:直角三角形斜边上的中线等于斜边的一半“) --12分 注:⑴过对角线交点O作OF⊥BC于F.延长FO交AD于H.于是OH⊥AD 由△ABC≌△DCB.得到△OBC是等腰直角三角形.OF=BC= 同理OH=AD=.高HF= ⑵过A作AF⊥BC于F.过D作DH⊥BC于H.由△AFC≌△DHB 得高AF=FC==5 ⑶
网址:http://m.1010jiajiao.com/timu3_id_438180[举报]
(创新题)“有两边相等的两个直角三角形全等”这个命题对与否,甲、乙、丙三位同学给出了如下论断:
甲:正确.因为若两边都是直角边,则用(S.A.S.)全等识别法就可以证它们全等.
乙:正确.因为若其中一边是直角边,另一边是斜边,则可用(H. L.)定理证全等.
丙:不正确.若一个三角形较长的直角边与另一三角形斜边相等,较短的直角边与另一三角形较长的直角边相等,则显而易见两个三角形不全等.
请你就这三个同学的见解发表自己的意见.
我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
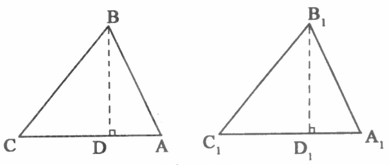
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1Cl,∠C=∠Cl.
求证:△ABC≌△A1B1C1.
(请你将下列证明过程补充完整.)
证明:分别过点B,B1作BD⊥CA于D,B1 D1⊥C1 A1于D1.
则∠BDC=∠B1D1C1=900,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,-
∴BD=B1D1.
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论.
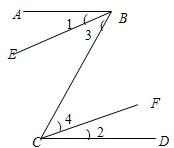 10、如图所示,已知∠1=∠2,若要证∠3=∠4,则需要( )
10、如图所示,已知∠1=∠2,若要证∠3=∠4,则需要( )