摘要： 我们知道:由于圆是中心对称图形.所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分. 探索下列问题: (1)在图11-2给出的四个正方形中.各画出一 条直线(依次是:水平方向的直线.竖直方 向的直线.与水平方向成45°角的直线和 任意的直线).将每个正方形都分割成面积 相等的两部分, (2)一条竖直方向的直线m以及任意的直线n. 在由左向右平移的过程中.将正六边形分成 左右两部分.其面积分别记为S1和S2. ①请你在图11-3中相应图形下方的横线上 分别填写S1与S2的数量关系式(用“< . “= .“> 连接), ②请你在图11-4中分别画出反映S1与S2 三种大小关系的直线n.并在相应图形下 方的横线上分别填写S1与S2的数量关系 式(用“< .“= .“> 连接). (3)是否存在一条直线.将一个任意的平面图形分割成面积相等的两部分?请简略说出理由.
网址：http://m.1010jiajiao.com/timu3_id_438095[举报]
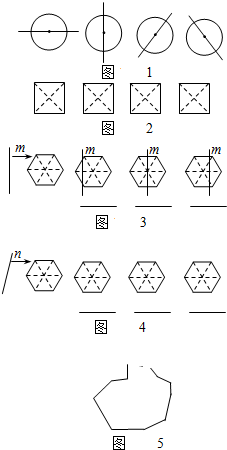
我们知道：由于圆是中心对称图形有，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分（如图1）。
探索下列问题：
(
1）在图2给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意直线），将每个正方形都分割成面积相等的两部分；
(2
）一条竖直方向的直线m以及任意直线n，在由左向右平移的过程中，将六边形分成左右两部分，其面积分别记为S1和S2。① 你在图3中相应图形下方的横线上分别填写S1与S2的数量关系式（用摚紨，摚綌，摚緮连接）；
② 请你在图4中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用摚紨，摚綌，摚緮连接）。
(3
）是否存在一条直线，将一个任意平面图形（如图11-5）分割成面积相等的两部分？请简略说明理由。
（2013•池州一模）我们知道：由于圆是中心对称图形，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分（如图1）．探索下列问题：
（1）在如图2给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2．
①请你在如图3中相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）；
②请你在如图4中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）．
（3）是否存在一条直线，将一个任意的平面图形（如图5）分割成面积相等的两部分？请简略说出理由．
我们知道：由于圆是中心对称图形，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分（如图1）．
探索下列问题：
（1）在如图2给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2．
①请你在如图3中相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）；
②请你在如图4中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）．
（3）是否存在一条直线，将一个任意的平面图形（如图5）分割成面积相等的两部分？请简略说出理由．
查看习题详情和答案>>
探索下列问题：
（1）在如图2给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2．
①请你在如图3中相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）；
②请你在如图4中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）．
（3）是否存在一条直线，将一个任意的平面图形（如图5）分割成面积相等的两部分？请简略说出理由．
查看习题详情和答案>>
我们知道：由于圆是中心对称图形，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分（如图1）
（1）在图2中给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2。
①请你写出图3中S1，S2的数量关系；（用“<”，“>”,“=”表示）
②请你在图4中分别画出反映S1与S2三种大小关系的直线n，并分别写出相应图形的S1与S2的数量关系式（用“<”，“=”，“>”连接）；
（3）是否存在一条直线，将一个任意的平面图形（如图5所示）分割成面积相等的两部分？请简略说出理由。
查看习题详情和答案>>
（2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2。
①请你写出图3中S1，S2的数量关系；（用“<”，“>”,“=”表示）
②请你在图4中分别画出反映S1与S2三种大小关系的直线n，并分别写出相应图形的S1与S2的数量关系式（用“<”，“=”，“>”连接）；
（3）是否存在一条直线，将一个任意的平面图形（如图5所示）分割成面积相等的两部分？请简略说出理由。
我们知道：由于圆是中心对称图形，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图(1))
探索下列问题：
(1)在图(2)给出的四个正方形中，各画出一条直线(依次是：水平方向的直线、竖直方向的直线、与水平方向成
角的直线和任意的直线)，将每个正方形都分割成面积相等的两部分；
(2)一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2．
①请你在图中相应图形下方的横线上分别填写S1与S2的数量关系式(用“＜”，“＝”，“＞”连接)；
②请你在图中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“＜”，“＝”，“＞”连接)．
(3)是否存在一条直线将一个任意的平面图形(如图)分割成面积相等的两部分？请简略说出理由．
