摘要：已知△ABC是边长为4的等边三角形.BC在x轴上.点D为BC的中点.点A在第一象限内.AB与y轴的正半轴相交于点E.点B.P是AC上的一个动点 求点A.E的坐标, 若y=过点A.E.求抛物线的解析式. 连结PB.PD.设L为△PBD的周长.当L取最小值时.求点P的坐标及L的最小值.并判断此时点P是否在(2)中所求的抛物线上.请充分说明你的判断理由.
网址：http://m.1010jiajiao.com/timu3_id_437527[举报]
已知△ABC是边长为4的等边三角形，BC在x轴上，点D为BC的中点，点A在第一象限内，AB与
y轴的正半轴相交于点E，点B（-1，0），P是AC上的一个动点（P与点A、C不重合）
（1）求点A、E的坐标；
（2）若y=-
x2+bx+c过点A、E，求抛物线的解析式；
（3）连接PB、PD，设L为△PBD的周长，当L取最小值时，求点P的坐标及L的最小值，并判断此时点P是否在（2）中所求的抛物线上，请充分说明你的判断理由． 查看习题详情和答案>>
y轴的正半轴相交于点E，点B（-1，0），P是AC上的一个动点（P与点A、C不重合）（1）求点A、E的坐标；
（2）若y=-
6
| ||
| 7 |
（3）连接PB、PD，设L为△PBD的周长，当L取最小值时，求点P的坐标及L的最小值，并判断此时点P是否在（2）中所求的抛物线上，请充分说明你的判断理由． 查看习题详情和答案>>
已知△ABC是边长为1cm的等边三角形，以BC为边作等腰三角形BCD，使得DB=DC，且∠BDC=120°，点M是AB边上的一个动点，作∠MDN交AC边于点N，且满足∠MDN=60°，则△AMN的周长为2
2
．
y轴的正半轴相交于点E，点B（-1，0），P是AC上的一个动点（P与点A、C不重合）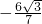
x2+bx+c过点A、E，求抛物线的解析式；
