摘要:如图.菱形ABCD的边长是2cm.E是AB的中点.且DE丄AB.则菱形ABCD的面积为 2cm2. 考点:菱形的性质,勾股定理. 分析:因为DE丄AB.E是AB的中点.所以AE=1cm.根据勾股定理可求出BD的长.菱形的面积=底边×高.从而可求出解. 解答:解:∵E是AB的中点. ∴AE=1. ∵DE丄AB. ∴DE==. ∴菱形的面积为:2×=2. 故答案为:2. 点评:本题考查菱形的性质.四边都相等.菱形面积的计算公式以及勾股定理的运用等.
网址:http://m.1010jiajiao.com/timu3_id_436011[举报]
(2012•无锡)如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.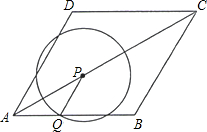 设点P运动的时间为ts.
设点P运动的时间为ts.
(1)当P异于A、C时,请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?
查看习题详情和答案>>
| 3 |
 设点P运动的时间为ts.
设点P运动的时间为ts.(1)当P异于A、C时,请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?
 如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.
如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.(1)求出经过A、D、C三点的抛物线解析式;
(2)是否存在时刻t使得PQ⊥DB,若存在请求出t值,若不存在,请说明理由;
(3)设AE长为y,试求y与t之间的函数关系式;
(4)若F、G为DC边上两点,且点DF=FG=1,试在对角线DB上找一点M、抛物线ADC对称轴上找一点N,使得四边形FMNG周长最小并求出周长最小值.
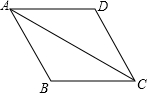 如图,菱形ABCD的边长为3,∠ABC=120°,则点D到AC距离长等于
如图,菱形ABCD的边长为3,∠ABC=120°,则点D到AC距离长等于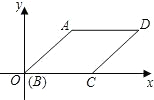 如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为
如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为 如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.