摘要:已知梯形ABCD中.AD∥BC.AB=AD.∠BAD的平分线AE交BC于点E.连接DE. (1)在下图中.用尺规作∠BAD的平分线AE.并证明四边形ABED是菱形. (2)若∠ABC=60°.EC=2BE.求证:ED⊥DC. 考点:梯形,菱形的判定与性质,作图-基本作图. 专题:作图题,证明题. 分析:(1)根据尺规作图:角的平分线的基本做法.可得到∠BAD的平分线AE,利用菱形的判定定理.即可证得, (2)根据直角三角形的性质定理.可得△EDC是直角三角形.即可得ED⊥DC, 解答:证明:(1)梯形ABCD中.AD∥BC. ∴四边形ABED是平行四边形. 又AB=AD. ∴四边形ABED是菱形, (2)∵四边形ABED是菱形.∠ABC=60°. ∴∠DEC=60°.AB=ED. 又EC=2BE. ∴EC=2DE. ∴△DEC是直角三角形. ∴ED⊥DC. 点评:本题考查了尺规作图及菱形.直角三角形的性质及判定.综合性较强.锻炼了学生的动手.动脑的能力.
网址:http://m.1010jiajiao.com/timu3_id_435798[举报]
如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E,设BE=x,△DEC的面积为y,问: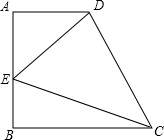
(1)你能找出y与x的函数关系吗?(写出自变量x的取值范围)
(2)△DEC的面积可能等于5吗?说明你的理由.
(3)探究何时△DEC的面积取得最大(小)值,并求出相应的最大(小)值. 查看习题详情和答案>>

(1)你能找出y与x的函数关系吗?(写出自变量x的取值范围)
(2)△DEC的面积可能等于5吗?说明你的理由.
(3)探究何时△DEC的面积取得最大(小)值,并求出相应的最大(小)值. 查看习题详情和答案>>
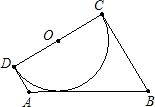 如图,已知梯形ABCD中,AD∥BC,∠C=90°,以CD为直径的圆与AB相切,AB=6,求梯形ABCD的中位线长.
如图,已知梯形ABCD中,AD∥BC,∠C=90°,以CD为直径的圆与AB相切,AB=6,求梯形ABCD的中位线长. 6、如图,已知梯形ABCD中,AD∥BC,AB=CD=AD,AC、BD相交于O点,∠BCD=60°,下列结论中正确的有:①梯形ABCD是轴对称图形;②BC=2AD;③梯形ABCD是中心对称图形;④AC平分∠DCB.( )
6、如图,已知梯形ABCD中,AD∥BC,AB=CD=AD,AC、BD相交于O点,∠BCD=60°,下列结论中正确的有:①梯形ABCD是轴对称图形;②BC=2AD;③梯形ABCD是中心对称图形;④AC平分∠DCB.( )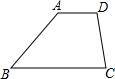 如图,已知梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,上底AD=4,腰DC=6,则下底BC长为
如图,已知梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,上底AD=4,腰DC=6,则下底BC长为 9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )
9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )