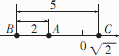摘要:. 考点:实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值. 分析:本题需先根据实数运算的顺序和法则.分别进行计算.再把所得的结果合并即可求出答案. 解答:解:﹣﹣2sin45°+0. =4﹣2+﹣+1. =3. 点评:本题主要考查了实数的运算.在解题时要注意运算顺序和公式的应用是本题的关键.
网址:http://m.1010jiajiao.com/timu3_id_435795[举报]
已知: 是一元二次方程
是一元二次方程 的两个实数
的两个实数 根.
根.
求: 的值.考点:实数的运算;零指数幂;负整数指数幂.
的值.考点:实数的运算;零指数幂;负整数指数幂.
专题:计算题.
分析:分别根据负整数指数幂、0指数幂、绝对值的性质及二次根式的化简计算出各数,再根据实数混合运算的法则进行计算即可.
解答:解:原式=2-1-3+2,
=0.
故答案为:0.
点评:本题考查的是实数的运算,熟知负整数指数幂、0指数幂、绝对值的性质及二次根式的化简是解答此题的关键.
答题:ZJX老师
已知: 是一元二次方程
是一元二次方程 的两个实数根.
的两个实数根.
求: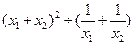 的值.考点:实数的运算;零指数幂;负整数指数幂.
的值.考点:实数的运算;零指数幂;负整数指数幂.
专题:计算题.
分析:分别根据负整数指数幂、0指数幂、绝对值的性质及二次根式的化简计算出各数,再根据实数混合运算的法则进行计算即可.
解答:解:原式=2-1-3+2,
=0.
故答案为:0.
点评:本题考查的是实数的运算,熟知负整数指数幂、0指数幂、绝对值的性质及二次根式的化简是解答此题的关键.
答题:ZJX老师
查看习题详情和答案>>
 是一元二次方程
是一元二次方程 的两个实数根.
的两个实数根.求:
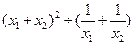 的值.考点:实数的运算;零指数幂;负整数指数幂.
的值.考点:实数的运算;零指数幂;负整数指数幂.专题:计算题.
分析:分别根据负整数指数幂、0指数幂、绝对值的性质及二次根式的化简计算出各数,再根据实数混合运算的法则进行计算即可.
解答:解:原式=2-1-3+2,
=0.
故答案为:0.
点评:本题考查的是实数的运算,熟知负整数指数幂、0指数幂、绝对值的性质及二次根式的化简是解答此题的关键.
答题:ZJX老师
查看习题详情和答案>>
已知: 是一元二次方程
是一元二次方程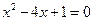 的两个实数
的两个实数 根.
根.
求: 的值.考点:实数的运算;零指数幂;负整数指数幂.
的值.考点:实数的运算;零指数幂;负整数指数幂.
专题:计算题.
分析:分别根据负整数指数幂、0指数幂、绝对值的性质及二次根式的化简计算出各数,再根据实数混合运算的法则进行计算即可.
解答:解:原式=2-1-3+2,
=0.
故答案为:0.
点评:本题考查的是实数的运算,熟知负整数指数幂、0指数幂、绝对值的性质及二次根式的化简是解答此题的关键.
答题:ZJX老师
 是一元二次方程
是一元二次方程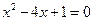 的两个实数
的两个实数 根.
根.求:
 的值.考点:实数的运算;零指数幂;负整数指数幂.
的值.考点:实数的运算;零指数幂;负整数指数幂.专题:计算题.
分析:分别根据负整数指数幂、0指数幂、绝对值的性质及二次根式的化简计算出各数,再根据实数混合运算的法则进行计算即可.
解答:解:原式=2-1-3+2,
=0.
故答案为:0.
点评:本题考查的是实数的运算,熟知负整数指数幂、0指数幂、绝对值的性质及二次根式的化简是解答此题的关键.
答题:ZJX老师